Inscription / Connexion Nouveau Sujet
DM sur Droite d'Euler
Bonjour , j'ai un dm a rendre dans quelques jours avec pour titre la Droite d'Euler ...
J'essaie de faire 1 , 2 questions en vain ... a croire que je n'ai pas été à l'école ..
Je suis en 2GT .
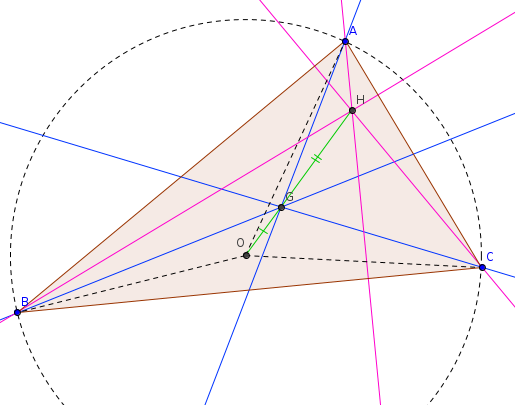
J'ai un triangle ABC n, h orthocentre , g centre de gravité , o centre du cercle circonscrit .
Je bloque déja à la premiere , il sagit d'émettre deux conjectures cocnernant les points g , h , o .. en déplacant a .
Merci d'avance
Bonjour,
as-tu cherché sur le web 3droite d'Euler" ?....
je suppose que tu utilises un logiciel de géométrie dynamique comme Géogebra...en déplaçant le sommet A, si tu as construit convenablement les points O, G et H, tu devrais constater qu'ils sont alignés
Donc , d'après vous , la réponse à la question : en déplaçant A quelles sont les 2 conjectures avec les points G , H , O ?
Ce serait que soit au G soit au 2/3 de OH et que OGH soient alignés ?
Merci d'avance
euh, ma compréhension de ton expression écrite n'est pas tout à fait à la hauteur, mais si tu veux l'exprimer ainsi, nul doute que ton prof va apprécier.
tu t'es relu ?
Pardon , effectivement je suis un peu fatigué ...
Donc ce que je voulais et que les 2 conjectures à démontrer après sont :
- G au 2/3 de OH
- O, G , H alignès
Suis je plus clair ?
Mais comment démontrer que ( CH ) et ( BA' ) sont parallèles ?
et bien on progresse
jusque là tu ne franchissais pas la barrière de la conjecture, et maintenant tu veux démontrer.
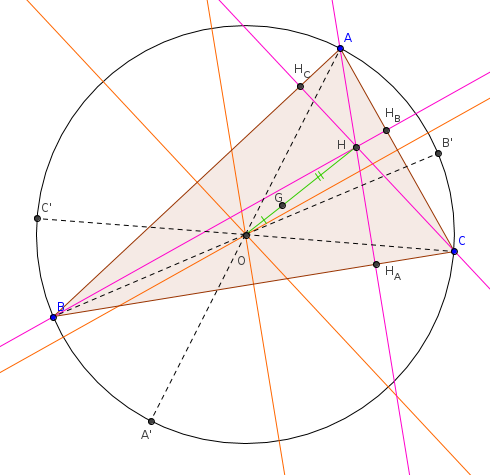
puis-je respectueusement te faire remarquer que si tu as défini A, B, C, O, H, G, tu n'as pas défini A' ?
j'ai écrit :
conjecture : il semble que g soit au tiers du segment [oh]
tu as traduit
- G au 2/3 de OH
tu dois vraiment être très fatigué
J'ai bien représenté mon point diamétralement opposé à A qu'est A' sur mon dessin de Geogebra . Pouvez vous m'éclairer sur quelle piste chercher ?
J'ai bien représenté
sûrement, mais tu n'en avais rien dit jusque là
j'apprécie que tu nous penses capable de lire à distance dans ton esprit, voire par dessus ton épaule.
mais j'ai peur que tu ne nous prêtes de trop grands pouvoirs.
donc O est le milieu du segment [AA']
et grâce à GeoGebra, peux-tu me dire ce que t'inspire l'angle ABA' ?
Oui je suis bien fatigué désolé , je me concentre .
Maintenant que les conjectures à démontrer sont trouvées , comment démontrer que (ch) et (ba') sont parallèles ?
Peut être avec les vecteurs et la loi de Chasles ?
alors justifie maintenant cette nouvelle conjecture, en plongeant dans tes souvenirs de classe de Quatrième, et ensuite compare les angles et
, où
est le pied de la hauteur issue de C
Je me casse la tête sur votre piste mais je ne trouve pas , est ce bien avec les angles alternes internes de même mesure ??
La hauteur est la droite qui passe par la sommet et perpendiculaire au côté opposé à ce sommet .
or toute si une droite est perpendiculaire à l'une , elle est perdenulaire à l'autre .
deux droites sont perpendiculaires à une meme troisième droite alors elles sont parallèles entre elles .
est ce la bonne piste ?
Cette question est faite , fallait il démontrer que ABA' = 90 ° selon Geogebra ?
Maintenant , il m'est demandé de démontrer que segments BC et HA' ont le même milieu . Sans me donner la solution , pouvez vous me dire quelle raisonnement suivre ?
j'aimerais bien que tu montres un peu plus d'assurance
ça ne te paraît pas clair ?
1) dans le plan, deux droites perpendiculaires à une troisième sont parallèles entre elles
2) dans un cercle, tout point X du cercle en dehors d'un diamètre YZ forme un triangle XYZ qui est rectangle en X
donc
- la hauteur (CH) est perpendiculaire à la droite (AB)
- le triangle ABA' est rectangle en B puisque B est sur le cercle de diamètre AA'
- donc la droite (A'B) est perpendiculaire à la droite (AB)
- donc les deux droites (CH) et (A'B) sont parallèles entre elles
l'art et la manière d'additionner 1 et 1
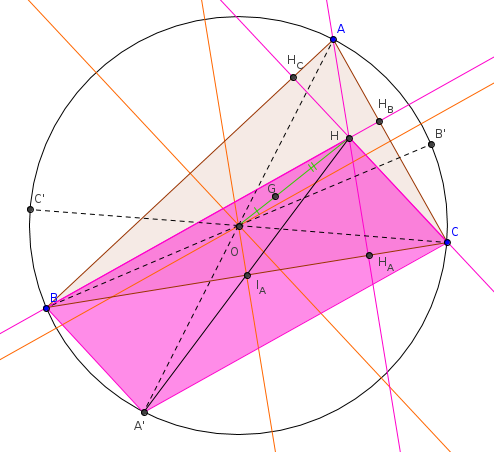
et pour la suite, puisque tu souhaites juste une indication, intéresse-toi aux deux droites (BH) et (A'C), puis au quadrilatère BHCA'
Je pense que cela pourrait être la relation vectorielle avec la loi du parallélogramme et avec les diagonales qui se coupent en leurs mileu , point I . est ce la bonne piste ?
On a prouvé que BA' et CH étaient parallèles , il reste donc à prouver que BH et A'C le sont aussi non ?
Pour ensuite dire la propriété des diagonales .. ?
J'ai encore besoin d'aide svp ..
BHA'c quadrilatère , or BA' etCH sont parallèles .
alors si dans un quadrilatère les côtés opposés sont parallèles , alors il s'agit d'un parallélogramme ?
pourquoi es-tu incapable de vérifier par toi-même si ton affirmation est vraie ou fausse
ce n'est pas que je refuse de te le dire, mais tu affirmais
Sans me donner la solution , pouvez vous me dire quelle raisonnement suivre ?
si je te donne le raisonnement, je te donne la solution
or tu n'arrives pas à t'auto-compléter.
bon, alors voilà :
(CH) hauteur issue de C donc
B sur cercle de diamètre AA' donc
donc
ça, tu y es finalement arrivé
(BH) hauteur issue de B donc
C sur cercle de diamètre AA' donc
donc
deux couples de droites parallèles forment effectivement un parallélogramme
A'BHC est un parallélogramme
et une caractéristique vue en Cinquième des parallélogrammes est que leurs diagonales se coupent en leurs milieux
donc les deux segment [BC] et [A'H], diagonales du parallélogramme A'BHC, se coupent en leur milieu, que j'ai appelé
Merci beaucoup pour cette réponse , si je manque de confiance quand j'essaie de formuler une réponse , c'est que je ne suis sur de rien .... C'est pour cela !
Encore merci
J'ai maintenant à en déduire que G est le cnetre de gravité du triangle AHA'.
- On sait que J milieu de AH'
- la médianne est la droite passant par J issue de A .
De même pour les autre côtés ..
Et donc le centre de gravité est le point d'intersection de ces médianes .
Besoin d'aide pour cette question car mon cours mon dit que le vecteur AG est egale au 2/3 du vecteur AJ , mais comment en déduire que G est le centre de gravité avec J milieu de A'H et O milieu de AA' .
Merci d'avance pour le coup de pouce !!
c'est que je ne suis sur de rien .... C'est pour cela !
eh bien il faut vite que tu apprennes à vérifier par toi-même
à l'ère d'Internet, il y a quand même de la matière.
je ne prétends pas que tu ne dois pas recourir à notre aide, mais retrouver la définition et les propriétés d'un parallélogramme, il est inconvenant que tu attendes qu'on te rassure sur ce point-là. Tu saisis la différence ?
J'ai maintenant à en déduire que G est le centre de gravité du triangle AHA'.
tout cela est bien intéressant, mais c'est la définition de l'énoncé : tu disais dans ton premier message que G était le centre de gravité, tu n'as pas besoin de le déduire
ce qu'il te faut déduire, montrer, c'est que G est bien, comme ta conjecture le prétend, au tiers du segment [OH]
- On sait que J milieu de AH'
Tout cela est bien intéressant, mais nulle part tu ne donnes la définition de H'.
- la médiane est la droite passant par J issue de A .
De même pour les autre côtés ..
Et donc le centre de gravité est le point d'intersection de ces médianes .
et alors ? ça ne fait pas de G un point de [OH]...
voici une démonstration purement géométrique du résultat attendu (il existe une démonstration vectorielle peut-être plus simple, mais c'est une question de goût)
dans le triangle A'AH, O est milieu de A'A, I_A est milieu de A'H
donc d'après de théorème de Thalès, est double de
prenons maintenant les deux segments et
on veut montrer qu'ils se coupent en G, mais on n'en sait encore rien. Alors appelons leur point d'intersection, nous allons montrer que
EST le centre de gravité
les triangles et
forment une configuration de Thalès en papillon, car
donc nous avons grâce à Thalès les rapports suivants :
mais nous venons de voir que est double de
donc
et finalement cette dernière relation nous permet d'établir que est au tiers de la médiane
: c'est une caractéristique du centre de gravité du triangle :
on vient d'établir que ce point , intersection de [OH] et de la médiane, est confondu avec
, centre de gravité du triangle
Thalès, pour finir, nous permet aussi d'écrire
ce qui permet d'établir que G est bien au tiers du segment [OH]
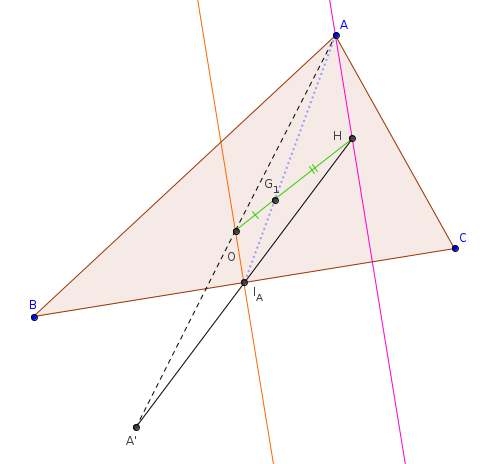
Encore une fois merci de votre aide apportée , j'espère en tirer des leçons pour mes futurs façons de raisonner devant des problèmes mathématiques . La dernière question est de prouver les conjectures du début , celle ou G est au tiers de la médiane c'est ok mais pour prouver l'alignement des points ... Je cherche , je pars sur la piste de la colinéarité
Désolé , je ne vois pas quelle parti de vos rasionnement vient prouver cet alignement ... la parti thalès papillon ?