Inscription / Connexion Nouveau Sujet
DM sur les dérivées de fonctions
Bonsoir, j'ai un devoir à faire, dont le sujet est le suivant:
"Soit f la fonction définie par f(x)=k* où k et r sont deux réels strictement positifs fixés. Dans un repère orthonormé, on considère la courbe
définie par la réunion des courbes des fonctions f et -f.
1. Déterminer le domaine de définition de f.
Soit x
. On considère le point M d'abscisse x et d'ordonnée positive se trouvant sur
. On appelle N le symétrique de M par rapport à l'axe des abscisses. Enfin, on appelle P le point de coordonnées (r;0). P se trouve donc aussi sur
.
On considère le triangle MNP et on note g(x) son aire.
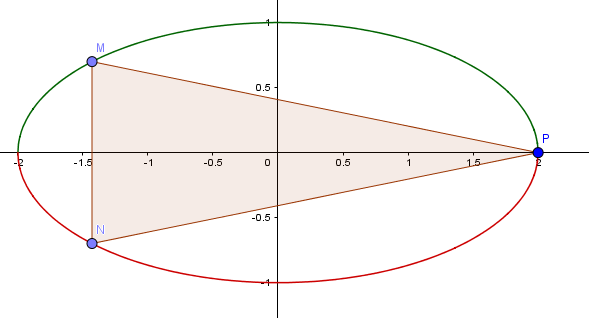
2. Faire une figure complète pour le cas k= 1/2 et r=2. On prendra pour unité 2 cm sur chaque axe.
3. Exprimer g(x) en fonction de x.
4. Calculer g'(x) sur privé des ses bornes et montrer que g'(x) =
5. Etudier les variations de g, dresser le tableau de variations complet et déterminer la valeur de x pour laquelle l'aire du triangle MNP est maximale. Préciser alors pour ce cas les coordonnées de M et N.
6. x est fixé à la valeur trouvée dans la question précédente. Dans le cas où k=1, que peut-on déduire du triangle MNP? Bien justifier."
Pour le moment j'ai fait les questions 1, 2 et 3:
J'ai [-r;r] pour le domaine de définition , et pour g(x) j'ai trouvé . Pour la question 4, j'ai abouti à g'(x)=
Je n'ai malheureusement pas réussi à montrer que g'(x) valait , et pour la question 5, je pense qu'il faut résoudre g'(x) mais je n'y arrive pas, quelqu'un pourrait-il m'indiquer la marche à suivre s'il vous plaît?
Bonsoir carita
je vous laisse poursuivre
Quelle plaie les calculatrices, il n'y plus maintenant de simplification !
Je ne vois pas comment simplifier la fraction, il faut développer le numérateur mais je ne vois absolument pas par où commencer...
anoukg, hekla t'a indiqué où faire la simplification :
tu as un facteur 2 au numérateur, et 2 au dénominateur : ils s'éliminent.
Je n'arrive pas à simplifier g(x), donc je vais me contenter de ce que j'ai trouvé, merci pour vos réponses!