Inscription / Connexion Nouveau Sujet
DM sur les logarithmes
Bonjour j'ai un DM sur les logarithmes et je voulais qu'on vérifie mes réponses mais aussi qu'on m'aide pour les deux dernières questions.
Voilà l'énoncé,
Pour tout nombre réel k strictement positif, on considère la fonction fk définie sur l'intervalle ]0; +
[ par fk(x)= ln(x)-kx2+1
1) Déterminer la limite de la fonction fk en 0.
2a) Démontrer que
b) En déduire la limite de la fonction fk en +
3) Montrer que pour tout nombre réel x strictement positif:
f'k(x)=
4) Pour un nombre réél k strictement positif, on donne ci-après le tableau de variation de la fonction fk:
(image plus bas)
Justifier les renseignements sur les variations de la fonction fk figurant dans ce tableau.
5) Déduire, du tableau de variation, le nombre de solutions de l'équation fk(x)=0 en fonction des valeurs de k.
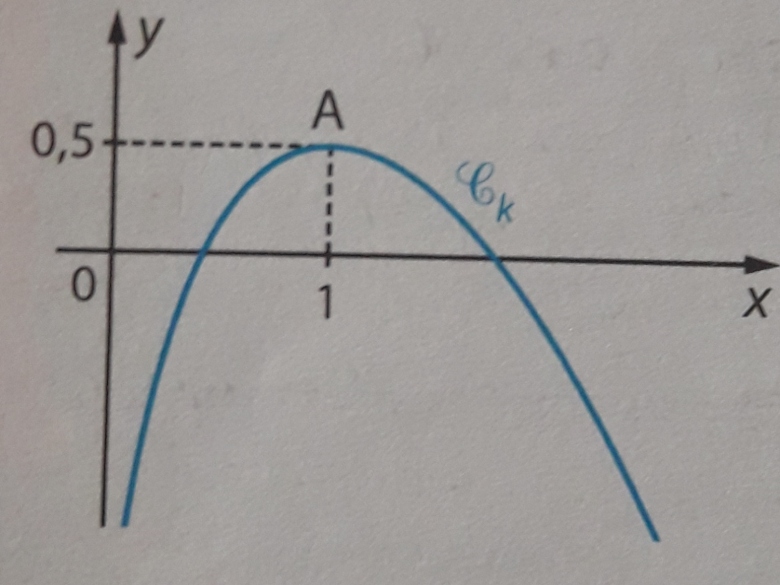
6) On a tracé ci-dessous la courbe Ck représentative d'une fonction fk pour une certaine valeur du nombre réel k strictement positif (courbe en bas).
Le point A(1;) appartient à la courbe Ck. Quelle est la valeur du nombre réel k correspondant ? Justifier la démarche.
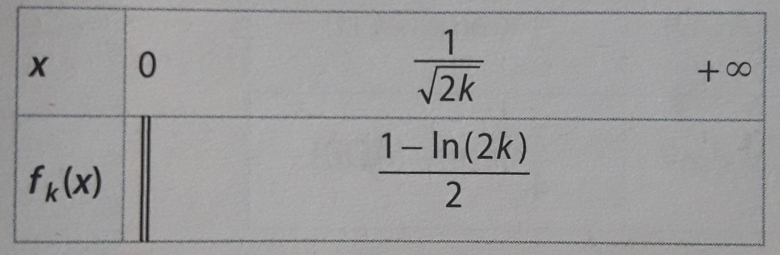
Pour la 1) j'ai trouve -
2a) J'ai trouvé 0 car les valeurs de x2 sont plus élevées que les valeurs de ln(x) en
b) J'ai eu -
3) J'ai eu bon à la fin j'ai =
4) en 0 j'ai mis - que ça monte jusqu'à
et que ça baisse jusqu'à -
. Mais je n'arrive pas à justifier
5) Je ne suis pas sûr de moi mais j'ai dit qu'il y'a une unique solution sur ]0; +[ et car f coupe qu'une fois l'axe mais je ne sais pas si y'a des choses à ajouter.
6) Je bloque
pour la 6 tu dois faire une équation.
si le point A(1;1/2) appartient à la courbe Ck alors si tu remplaces x par 1 dans ln(x)-k*x^(2)-1, tu trouves 1/2.
tu as donc: ln(1)-k*1^(2)-1= 1/2
<=> 0-k*1-1=1/2
tu peux continuer je pense.
Je crois que t'as fais une boulette parce que c'est pas -1 mais +1 donc ln(1)-k(1)2+1=1/2. On a k=3/2 et non -3/2
bonsoir
pour 4) tu as étudié le signe de la dérivée ?
sinon, ce que tu dis est exact.
5) sauf erreur de ma part, il n'y a pas toujours de solutions à fk(x) = 0 :
ça dépend de la valeur de k (ordonnée de l'extremum) : 0 , 1 ou 2 solutions.
5) d'après le tableau de variation,
le nombre de solutions de fk(x) = 0 va dépendre de la valeur de
si cette ordonnée est <0 alors pas de solution;
si =0 alors 1 solution;
si >0 alors 2 solutions.
quelle inéquation dois-tu donc poser et résoudre ?
attention tu as fait une erreur de recopie avec latex.
le principal c'est que tu poses la bonne inéquation sur ton papier 



