Inscription / Connexion Nouveau Sujet
Dm Terminal S exponetielle
Donc voilà , premier DM sur les exponentielles , et je maîtrise pas à 100% ^^ pourtant je suis pas si mauvais en maths.
Alors : on a une fonction P, définie sur [0; +inf [ par P (x) = 100 * e^(-0.015x)
En gros x c'est l'épaisseur en cm d'une plaque de verre qui laisse passe un pourcentage P (x) de lumière
Donc voilà les questions ou j'ai eu du mal
1) trouver la limite en +inf
P (x) = 100 * e^-0.015x
lim (-0.015x) = -inf
donc lim (e^-0.015x) = 0
(je suis pas du tout sur de moi sur ce que je viens de faire en haut ^^ )
lim P (x) = 100*0 = 0
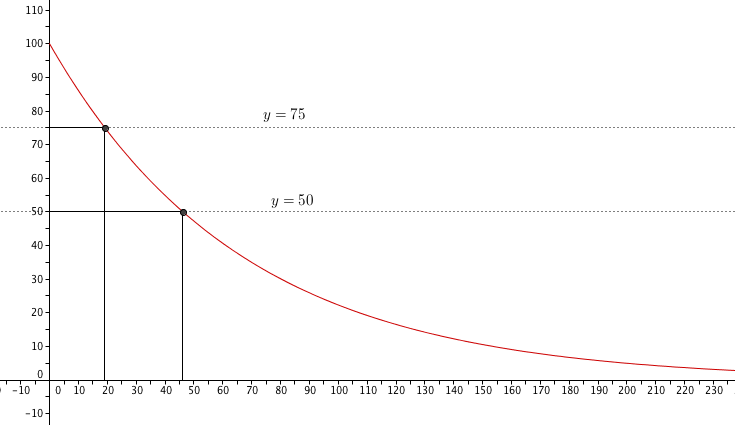
2) lire avec la précision permise par le graphique l'abscisse du point d'ordonnée 50 et 25
je trouve 46 et 92
Bon la j'ai pas eu trop de mal mais j'ai voulu mettre cette question parce que elle a un lien avec LA QUESTION difficile du Dm
4a : on a un algorithme
Entré : saisir k qui appartient à [0;100]
saisir n qui appartient à N*
initialisation : a prend la valeur 0
traitement : tant que P (a) >k
a prend la valeur a+10^-n
fin tant que
Sortie
Afficher à
Donc la question c'est : quel est le rôle de l'algorithme
Tous mes potes me disent sur c'est trouver l'épaisseur de la plaque qui laisse passer k% de lumière ; mais je pense qu'il y a un truc derrière.
Ma réponse : il affiche la plus petite épaisseur a (en cm et qui a pour précision 10^-n) telle que la plaque laisse passe plus de k% de la lumière.
Je suis pas trop sur de moi...
Et enfin ; LA QUESTION DIFFICILE DU DM ( ou plutôt une question chelou que j'ai pas trop compris ^^ ) :
Sí on connaît à l'avance une valeur de a non précise donnée par lecture graphique de la question 2, proposer une modification de cet algrotythme qui permette d'accélérer l'affichage demandé.
J'ai pensé à ce que a prenne directement la valeur aproximative au lieu de commencer par a=0, et qu'au fur et à mesure il augmente ou il baisse jusqu'à atteindre la précision demandé par n. Mais je sais pas comment modifier l'algorithme pour qu'il fasse cela , et puis de toute façon je pense que je me trompe de piste.
Donc voilà , quelqun pourrait m'apporter son aide; de préférence avant ce soir silvouplait 
Okay donc voila l'énoncé dans son intégralité :
Le plastique acrylique, plus résistant que le verre, est une matière transparente laissant passer la lumière.
Pour calculer le pourcentage de lumière traversant une plaque de plastique acrylique, on utilise la fonction P définie sur [0; +inf[ par :
P(x) = 100 * e^-0.015
où x est l'épaisseur en cm de la plaque
1) Déterminer la limite de P quand x tend vers +inf. Interpreter ce résultat.
2) Lire avec la précision permise par le graphique, l'épaisseur d'une plaque :
a) laissant passer 50% de la lumière
b) bloquant 75% de la lumière
3) étudier le sens de variation de P, interpreter ce résltat.
4) a : quel est le rôle de l'algorithme ci dessous :
Entrée:
saisir k qui appartient à [0;100]
saisir n qui appartient à N*
initialisation : a prend la valeur 0
traitement : tant que P (a) >k
a prend la valeur a+10^-n
fin tant que
Sortie
Afficher a
b: coder cet algorithme dans le langage de votre calculatrice
c: faire fonctionner cet algorithme
pour k=50 et n=2
pour k=25 et n=1
Interpreter les résultats
d: Si on connaît à l'avance une valeur de a non précise donnée par lecture graphique de la question 2, proposer une modification de cet algorithme qui permette d'accélérer l'affichage demandé.
Bon j'espère que cela vous aidra à comprendre
Ah merci Jedoniezh , donc si j'ai bien compris, c fait
P(x) = 100 * e^-0.015x
P(x) = 100/e^0.015x
lim (e^0.015x) = +inf
lim P(x) = 0 (par quotient)
) Déterminer la limite de P quand x tend vers +inf. Interpreter ce résultat.
Plus l'épaisseur du verre augmente, et moins la lumière passe.
2) Lire avec la précision permise par le graphique, l'épaisseur d'une plaque :
a) laissant passer 50% de la lumière
Voir figure :
b) bloquant 75% de la lumière
Voir figure :
3) étudier le sens de variation de P, interpreter ce résltat.
est dérivable sur
et :
Petite erreur de frappe.
1) Déterminer la limite de P quand x tend vers +inf. Interpreter ce résultat.
Il n'est pas des plus clairs cet algorithme ....
Entrée:
saisir k qui appartient à [0;100] ==> on fixe le % de lumière que l'on souhaite faire passer, soit P(x), et en l'occurence ici ce sera P(a)
saisir n qui appartient à N* ==> on fixe le pas d'avancement entre la 2 valeurs de . Rappelons que l'épaisseur
est exprimée en cm, donc si on prend
, alors
donnera une progression de
en mm, si on prend
, la progression sera de 1 micron entre 2 vleurs de
initialisation : a prend la valeur 0 donc P(a)=P(0)=100
traitement : tant que P (a) >k On regarde si P(a) est supérieur à ce qu'on à fixer comme valeur en début d'algoritme
a prend la valeur a+10^-n ==> on fait progresser la valeur de de l'épaisseur qu'on a fixée grâce à
fin tant que
Sortie
Afficher a
Tous mes potes me disent sur c'est trouver l'épaisseur de la plaque qui laisse passer k% de lumière ; mais je pense qu'il y a un truc derrière. ==> en quelque sorte oui
Ma réponse : il affiche la plus petite épaisseur a (en cm et qui a pour précision 10^-n) telle que la plaque laisse passe plus de k% de la lumière. ==> c'est plus cela oui
Mais à mon sens, ce serait plus "Cet algorithme permet de donneer l'épaisseur de verre du carreau, à la précision de près, ce afin d'être conforme à l'opacité fixée à l'avance."
b: coder cet algorithme dans le langage de votre calculatrice
A toi de voir avec ta calculatrice (pour ma part je ne l'ai pas programmée)
Idem pour la c).
d: Si on connaît à l'avance une valeur de a non précise donnée par lecture graphique de la question 2, proposer une modification de cet algorithme qui permette d'accélérer l'affichage demandé.
J'ai pensé à ce que a prenne directement la valeur aproximative au lieu de commencer par a=0
Oui, c'est tout à fait cela. Pour être plus précis, je dirais de rentrer une valeur de
Pardon :
Oui, c'est tout à fait cela. Pour être plus précis, je dirais de rentrer une valeur de légèrement supérieure à celle que l'on lit sur le graphique.
Bonjour,
Pour la dernière question :
"Si on connaît à l'avance une valeur de a non précise donnée par lecture graphique
telle que P(a)=k..."
on veut a avec la précision e=10-n, alors que a est donné graphiquement à d près
la méthode par dichotomie est la plus facile à mettre en oeuvre et assez rapide, moins rapide cependant que la méthode de Newton (voir wikipedia pour ces méthodes d'approximation)
Oh merci beaucoup Jedoniezh , donc si j'ai bien compris , le nouvel algorithme donne :
Entrée:
saisir k qui appartient à [0;100]
saisir n qui appartient à N*
saisir x
initialisation : a prend la valeur x
traitement : tant que P (a) >k
a prend la valeur a+10^-n
fin tant que
Sortie
Afficher a
Bonjour,
Voici d'abord votre algorithme écrit en Python avec k, n et a choisis :
(après # se trouve un commentaire dans le code)
J'ai introduit un compte du nombre d'itérations effectuées
from math import * # ceci introduit la constante e
def P(x): # définition de f(x)
return 100 * e**(-0.015*x) # les 2 ** disent élever à la puissance
k=75
n=3
a=18
compte=0
while(P(a) > k):
a+=10**(-n)
compte +=1
print("a =",a," nombre d'itérations =",compte)
Le résultat imprimé est :
a = 19.179000000001 nombre d'itérations = 1179
Et maintenant le même calcul par dichotomie
précision=10**(-n)
a=18 # a est choisi tel que P(a) >k
b=21 # b est choisi tel que P(a) <k
compte=0
while b-a > précision:
m=(a+b)/2
if P(m)>k:
a=m
else:
b=m
compte+=1
print("a =",a," nombre d'itérations =",compte)
Le résultat imprimé est :
a = 19.178466796875 nombre d'itérations = 12 : Comparez bien 1179 et 12 !
ATTENTION dichotomie adaptée à une courbe décroissante, le cas général est plus complet....



