Inscription / Connexion Nouveau Sujet
DM triangles
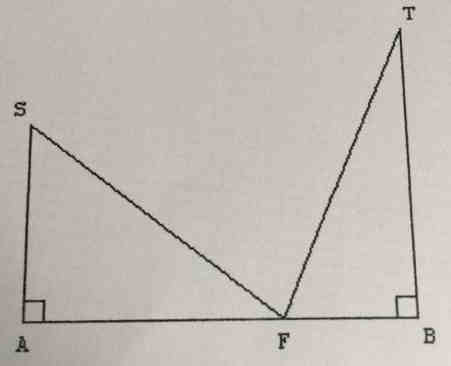
Bonjour pouvez vous m'aider sur ce problème : une figure représente deux triangles rectangles. AB=4, AS=2 et BT=3. Existe-t-il un point F du segment [AB] situé à la même distance de S et T. (Préciser sa position.
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
il te faudra redimensionner ton image avec paint ou autre logiciel....
Alors si ton énoncé est correct, on cherche à savoir s'il existe un point C sur [AB] tel que CS = CT.
Autrement dit, on cherche à savoir s'il existe , avec:
(1)
(2)
(1) est équivalent en passant au carré à :
et en développant avec (2):
Ensuite, en prenant les valeurs que tu me donnes, je peux choisir une base et dire que:
donc en développant les normes:
Soit:
Soit:
Soit:
Donc on a bien trouvé un lambda répondant à la question (sauf erreur de calcul de ma part)
Donc la réponse est oui, position en
bonjour antoinexp, en seconde il va falloir trouver une autre formulation...rien de tout ça n'a été vu manifestement....
Bonjour ;
Soit O le milieu de [A,B] ;
on a le triangle ASB rectangle en S , donc : OA = OB =OS ,
et le triangle ATB rectangle en T , donc OA = OB = OT ,
donc OS = OT , donc le point cherché est O .
En positionnant F sur [AB] on obtient deux triangles rectangles ASF rectangle en A et FTB rectangle en B.. le point F ne peut être au centre de [AB] puisque AS=2 et BT=3... Merci antoineexp mais effectivement ça n'a pas été vu 😥
Ok bah, les calculs sont les mêmes, il faut juste prendre un point de vue géométrique et pas algébrique:
_ SAC est rectangle en A, donc
_ BCT est rectangle en B, donc
ensuite, on veut SC = CT, donc:
avec AS=2, BT=3, AC+BC=4
donc:
Et voilà.
Ok, c'est plus simple.
donc:
Pardon,
et donc en développant on trouve aussi
Ok c'est plus simple, mais il faut connaître le théorème de pythagore donc bon.
Bonsoir ;
Puisque l'énoncé n'était pas clair , les résultats que j'ai donnés sont pour un exercice
autre que celui-ci .
Pour la version de l'énoncé pour laquelle vous avez optée, on trouve .
Puisque la figure n'est pas disponible, je présume en premier lieu que S et T sont du même côté
de la droite (AB) , donc on pose que T' est symétrique de T par rapport à (AB) ,
donc suivant cette figure on applique le théorème de Thalès aux triangles
FAS et FBT' , qui donne : donc 8 - 2 AF = 3AF
donc 8 = 5 AF donc .
Si maintenant S et T ne sont pas du même côté de la droite (AB),
on applique la même démarche sans passer par le symétrique de T .
Si la figure était disponible, les choses auraient été plus simples .
Je faisais le calcul sans retomber sur mes pattes, je commençais à me poser trop de questions., le mal de tête. Tu peux développer la dernière partie pour que je vois si je suis bon 😅 Merci en tout cas de m'accorder de ton précieux temps .. début d'année un peu tendu mais je lâcherai pas l'affaire..
Navré mais un problème d'ordinateur ne me permet pas de poster la figure, j'utilise donc le téléphone.. une photo est trop lourde malheureusement
Bonsoir ;
Puisque T' est le symétrique de T par rapport à B , donc (BT') est perpendiculaire à (AB),
et puisque (AS) est aussi perpendiculaire à (AB) donc (AS) est parallèle à (BT') ,
donc par la deuxième configuration du théorème de Thalès on a :
donc donc
.
Bonsoir aymanemaysae,
Merci de ta contribution, mais tu devrais faire plus attention aux énoncés des utilisateurs du forum, et ce en plus de ne pas négliger les réponses précédentes.
Donc relis attentivement l'énoncé de Speedyosc, et dis moi où tu as vu qu'on demandait d'aligner les points S, F, et T'.
Speedyosc: la question n'est pas d'avoir S, F, et T' alignés, mais SF = FT' = FT.
Pour développer le calcul:
Merci Antoine c'est tout à fait clair, net et précis. Je vais refaire d'autres scénarios pour voir si j'intègre bien la méthode. Un grand merci à tous et une excellente soirée.
Avec ce résultat j'obtiens FT=4 mais SF = 2,6.. 😥
Qu'est-ce que tu n'as pas compris dans ma solution pour partir sur la fausse solution de aymanemaysae ?
Tu ne vois pas que si tu appliques cette ânerie, avec Thalès tu vas obtenir SF/FT = AS/BT = 2/3?