Bonjour,
j'ai un DM à faire mais je ne comprends pas grand chose voici l'énoncé:
Dans ce problème , n est un entier naturel tels que
Une variable aléatoire X prends toutes les valeurs entières de 1 à n
Partie A
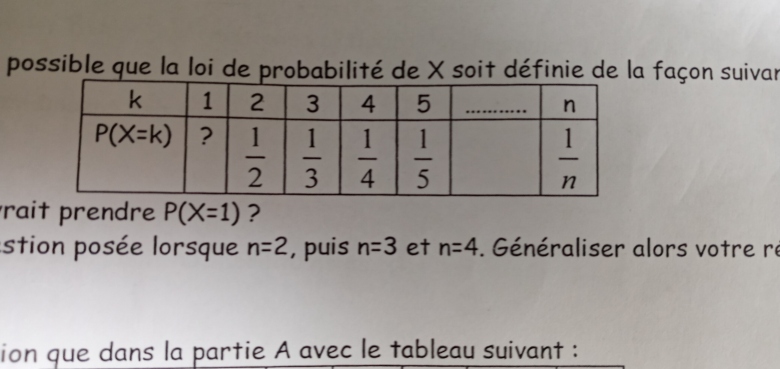
On se demande s'il était possible que la loi de probabilité de X soit définit de la façon suivante : tableau 1
1)Quelle valeur devrait prendre P(X=1)
2)Répondre à la question posé lorsque n=2, puis n=3 et n=4. Généraliser  alors votre réponse

Partie B
On se pose la même question que dans la partie A pour le tableau suivant: tableau 2
1) A l'aide de la calculatrice, calculer la somme ² pour n=10, pour n=100 et n=1000
2) On admet que quel que soit la valeur de n=>2; La somme ²  reste majorée par 0,65. Répondre à la question posée
3) Ecrire une fonction python qui permet, pour chaque  valeur de , et de retourner E(X).

Pour la partie A je pense avoir réussi.
1) J'ai trouver que P(x=1) devrait prendre la valeur de 0.  j'ai utiliser cette formule P(x=k)= p^k (1-p)^n-k
j'ai fait donc P(x=1)= 1¹ (1-p)^n-1
2) J'ai utiliser la même formule pour les autre en remplaçant le n et gardant k=1. Pour n=2 je trouve ainsi  =1/2 , pour n=3 je trouve n=4/9 et pour n=4 je trouve 27/4. Comme généralisation je trouve ((n-1)/n)^n-1.
Partie B c'est là que je comprends pas.
1) ² pour n=10 je trouve 0.54, pour n=100 je trouve 0.63, et pour n=1000 je trouve 0.64.
2) la question 2 je ne comprends pas quand elle me dit de répondre à la question posée
3) Python je suis nul, j'ai essayé mais rien ne fonctionne.
Cordialement