Inscription / Connexion Nouveau Sujet
Droite de Simson
Bonjour,
J'ai un exercice que je n'arrive pas à résoudre entièrement. Quelqu'un peut-il m'aider svp?
ABC est une triangle quelconque, de cercle C.
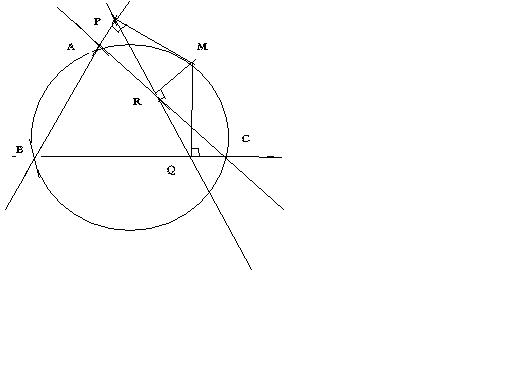
M est un point queconque de ce cercle, et les points P,Q et R sont ses projetés orthogonaux sur les côtés (AB), (BC) et (CA).
Les points P, Q et R sont alignés (la droite qui les contient s'appelle droite de Simson relative au point P)
a) Montrer que les points C,Q,R et M sont cocyliques
(J'ai démontré en m'appuyant sur un livre de Maths car je n'ai pas eu de cours)
En déduire que l'angle MRQ = 180°- angle BCM
b) Montrer que les points A,P, M et R sont cocycliques.
En déduire que angle PRM =180°- angle BAM
c) En utilisant la cocyclicité des points B,A,M etC montrer que angle BAM = 180°-angle BCM
d) Calculer l'angle PRQ puis conclure
Si une personne pouvait me donner quelques indications ce serait super sympa
Merci d'avance
Bonjour,
J'ai un exercice que je n'arrive pas à résoudre entièrement. Quelqu'un peut-il m'aider svp?
ABC est une triangle quelconque, de cercle C.
M est un point queconque de ce cercle, et les points P,Q et R sont ses projetés orthogonaux sur les côtés (AB), (BC) et (CA).
Les points P, Q et R sont alignés (la droite qui les contient s'appelle droite de Simson relative au point P)
a) Montrer que les points C,Q,R et M sont cocyliques
(J'ai démontré en m'appuyant sur un livre de Maths car je n'ai pas eu de cours)
En déduire que l'angle MRQ = 180°- angle BCM
b) Montrer que les points A,P, M et R sont cocycliques.
En déduire que angle PRM =180°- angle BAM
c) En utilisant la cocyclicité des points B,A,M etC montrer que angle BAM = 180°-angle BCM
d) Calculer l'angle PRQ puis conclure
Si une personne pouvait me donner quelques indications ce serait super sympa
Merci d'avance
*** message déplacé ***
Salut fusionfroide
Oui, je viens de regarder le problème mais je ne vois rien qui puisse m'aider a déduire une valeur d'angle
Merci pour ta réponse
s'il vous plait aider moi pour le a) et je trouverais pour le reste, il me faut juste une petite expilcation pour angle MRQ = 180°- BCM
Merci à tous
coucou
y a t il une personne pour m'aider
svp c'est pour demain et je planche depuis pas mal de temps
merci
Bonjour,
J'ai un exercice que je n'arrive pas à résoudre entièrement. Quelqu'un peut-il m'aider svp?
ABC est une triangle quelconque, de cercle C.
M est un point queconque de ce cercle, et les points P,Q et R sont ses projetés orthogonaux sur les côtés (AB), (BC) et (CA).
Les points P, Q et R sont alignés (la droite qui les contient s'appelle droite de Simson relative au point P)
a) Montrer que les points C,Q,R et M sont cocyliques
(J'ai démontré en m'appuyant sur un livre de Maths car je n'ai pas eu de cours)
En déduire que l'angle MRQ = 180°- angle BCM
b) Montrer que les points A,P, M et R sont cocycliques.
En déduire que angle PRM =180°- angle BAM
c) En utilisant la cocyclicité des points B,A,M etC montrer que angle BAM = 180°-angle BCM
d) Calculer l'angle PRQ puis conclure
Si une personne pouvait me donner quelques indications ce serait super sympa
Merci d'avance
MRC est un triangle rectangle en R donc l'hypoténuse est MC
MQC est un triangle rectangle en Q donc l'hypoténuse est aussi MC
Ils sont tous les 2 inscrits dans un cercle de diamtre MC donc C,Q,R,M sont cocycliques
En déduire que l'angle MRQ = 180°- angle BCM
S'il vous plait un peu d'aide
merci
M se projecte sur BC perpendiculairement , sur AC idem. donc les angles formés sont des angles droits.
MRQ = 180°- angle BCM <=> MRQ+BCM = 180°
MRC est un angle droit.
MQB est un angle droit.
Leur Somme = 180°
On sait de plus que : MRC = MRQ+CRQ , MQB = BCM+CMQ en remplaceant on a MRQ+CRQ+MQB-CMQ =180° CRQ = CMQ donc MRQ+BCM =180°
Ne doit-on pas passer par le fait que le quadrilatère inscrit au cercle C ait une sommes des angles égale à 360° ?
Bonjour,
Tu me dis comment tu as fait en 1)a), puis je t'aide pour la suite, d'accord ?
Nicolas
*** message déplacé ***
moi ossi g un travail sur la droite de Simson
la question est montrer que les points C,Q,R et M sont cocycliques (sa jy arrive mais apré)
montrer que MRQ= 180 - BCM
si qqn a réussi a le résoudre parce ke la je coince
*** message déplacé ***
Bonjour,
Le SMS est interdit sur ce forum. Merci d'en tenir compte.
Somme des angles dans le quadrilatère MRQC :
MRQ + RQC + BCM + CMR = 360° (1)
Angles inscrits sur le cercle CQRM :
RQC = 180° - CMR (2)
On soustrait (2) à (1) :
MRQ + BCM = 180°
MRQ = 180° - BCM
*** message déplacé ***
Merci beaucoup cela ma fait avancer d'un grand pas.
Désolé pour le message écrit en SMS.
J'ai une dernière question à poser!
A et B sont deux points d'un cercle de centre O, E est un point du petit arc AB, F point du grand arc AB.
Montrer que les angles AEB et AFB sont supplémentaire.
Là j'ai mis que dans un quadrilataire les angles opposés sont supplémentaires.
Est-ce suffisant, ou y a-t-il une autre démonstration?
*** message déplacé ***
"Quadrilataire" ou quadrilatère ? 
Je suis surpris que tu poses cette question, car exactement la même propriété que mon "
Angles inscrits sur le cercle CQRM :" ci-dessus.
"Là j'ai mis que dans un quadrilataire les angles opposés sont supplémentaires."
C'est faux. Les angles opposés d'un quadrilatère ne sont pas forcément supplémentaires ! Il suffit de faire une figure pour s'en rendre compte. Tu peux donner aux angles opposés la mesure que tu veux.
L'angle AEB intercepte le grand arc AB, donc AEB = (1/2) AÔB rentrant
L'angle AFB intercepte le petit arc AB, donc AFB = (1/2) AÔB saillant
Or AÔB rentrant + AÔB saillant = 360°
En divisant membre à membre par deux, on obtient :
AEB = AFB = 180°
Nicolas
*** message déplacé ***
Pour l'explication, là je suis en seconde et je n'ait pas encore entendu parlé d'angle rentrant et saillant. Mais sa m'apprends.
Sinon j'ai une autre explication :
Si on note E' le point diamétralement opposé à E.
A est un point du cercle de diamètre [EE'], donc AEE' est un triangle rectangle en A
B est un point du cercle de diamètre [EE'], donc BEE' est un triangle rectangle en B
On sait que la somme des angles aigus dans un triangle sont complémentaires :
AEE'+ AE'E = 90° et BEE'+BE'E = 90°
On ajoute les deux résultats
AEB + AE'B = 180°
l'angle inscrit AE'B intercepte l'arc AB et l'angle inscrit AFB intercepte l'arc AB donc ils ont la même mesure.
donc AE'B = AFB
AEB + AE'B = 180°
AEB + AFB = 180°
Donc on a bien deux angles supplémentaires
Voilà ce que j'ai pu trouver
Bonjour,
je reviens a ce que vous avez dit sur les droites de simson pour calculer MRQ = 180 - BCM
Comment sait on que :
Angles inscrits sur le cercle CQRM :
RQC = 180° - CMR?
POuvez vous m'aider
merci
b) Montrer que les points A,P, M et R sont cocycliques.
En déduire que angle PRM =180°- angle BAM
c) En utilisant la cocyclicité des points B,A,M etC montrer que angle BAM = 180°-angle BCM
d) Calculer l'angle PRQ puis conclure
Il faut absolument m'aider sé pour demain alors svp aider moi ..
ABC est une triangle quelconque, de cercle C.
M est un point queconque de ce cercle, et les points P,Q et R sont ses projetés orthogonaux sur les côtés (AB), (BC) et (CA).
Les points P, Q et R sont alignés (la droite qui les contient s'appelle droite de Simson relative au point P)
b) Montrer que les points A,P, M et R sont cocycliques.
En déduire que angle PRM =180°- angle BAM
c) En utilisant la cocyclicité des points B,A,M etC montrer que angle BAM = 180°-angle BCM
d) Calculer l'angle PRQ puis conclure
Si une personne pouvait me donner quelques indications ce serait super sympa
Merci d'avance
Voilà la figure