bonsoir,
peux-tu nous poster une figure?

Il n y en avait pas mais j en ai fait une en suivant point par point l énoncé et en prenant N et M au hasard sur le cercle
Par contre je ne sais pas comment importer une image sur ce forum 😃

dans la mesure où R appartient à la droite (MN), il va être bien difficile de démontrer que (RT) et (MN) sont parallèles

Ouais c'est ce que je me dis mais l'énoncé est bien celui ci (par contre R appartient non seulement a (MN) mais aussi a (AB)

Du coup tu sais vraiment pas comment je pourrai faire ? 😊

ben non
est-ce un exo du livre ?

Bonjour,

il doit y avoir une faute de frappe ou même d'impression la consigne étant très certainement

Démontrer que (ST) et (MN) sont parallèles



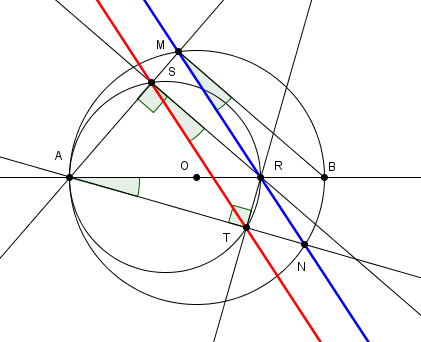
problème intéressant où j'ai fait figurer en plus tout ce qu'il faut pour faire la démonstration (quelques angles inscrits, cercle et segment supplémentaire)


à vous ....

Oui c'est ça je suis gogole j'ai fais LA faute de frappe a ne pas faire 😁

Ou pourrai je trouver vos indications?

sur ma figure

commencer par prouver que A, S, R et T sont cocycliques et donc l'existence même du cercle que j'ai ajouté est justifiée.
ensuite dans ce cercle on a une magnifique paire d'angles inscrits
ensuite ... pareil mais sur l'autre cercle
les trois angles marqués sont donc égaux.

ensuite justifier pourquoi MB est parallèle à SR
et là c'est fini ou presque
on peut pinailler la fin en rédigent ça "béton" par des angles alternes internes.

mathafou ?

je pense que ces histoires d'angles inscrits et de points sur un même cercle sont plus frais dans l'esprit de votre soeur que dans le vôtre
mes indications devraient suffire.
ce qui manquait dans cet exo était un "plan d'attaque", je l'ai donné.

Merci beaucoup et oui c'est bon j'ai compris des que tu mas expliqué 😊