Inscription / Connexion Nouveau Sujet
du cercle au triangle rectangle
Bonjour
Est-ce que quelqu'un peux me dire si mon exercice est bon
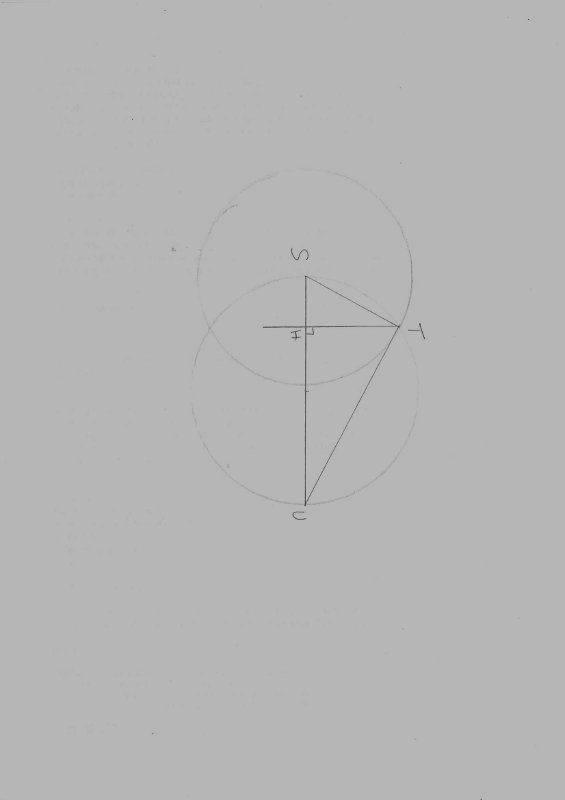
A. avec la règle graduée et le compas, construire un triangle STU rectangle en T tel que SU = 8,5 cm et ST= 4cm.
B. H est le pied de la hauteur issue de T.
Quels sont le centre et le rayon du cercle circonscrit au triangle UTH ?
Ma réponse
On sait que [TH} est la hauteur issue du point T dans le triangle TSU donc le triangle THU est rectangle en H.
Or si un triangle est rectangle alors l'hypoténuse est un diamètre de son cercle circonscrit.
Donc le cercle circonscrit a pour centre le point 0 milieu de l'hypoténuse [TU] et pour rayon la moitié de la longueur de l'hypoténuse, c'est-à-dire OT=OU= 1/2 TU
Je n'arrive pas à envoyer mon dessin
J'ai trace un cercle en prenant le milieu de TU est-ce exact
merci d'avance
Bonjour,
On te demande d'abord de construire le triangle STU.
Tu sais que le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse.
tu places donc un segment SU
tu mesures son milieu (mais le plus exact est de le placer au compas. Pour cela tu construis la lmédiatrice de [SU] et son intersection avec [SU] fixe avec précision le milieu.)
Tu traces en suite deux cercles
l'un de diamètre [SU]
l'autre de centre S et de rayon 4cm.
leurs intersections te donnent 2 points T possibles (symétriques par rapport à (SU))
ta réponse à la seconde question est juste mais il faut que tu calcules TU pour avoir le rayon que l'on te demande
Et pour cela , tu te sers du théorème de Pythagore que tu as certainement appris
Dans le triangle STU, c'est SU qui est l'hypoténuse, puisqu'il est rectangle en T.
Ton calcul de TU n'est donc pas bon.
Comment as-tu construit ce triangle ? Cela n'apparaît pas sur ta figure.
il y a quelque chose que je ne comprend pas pourquoi SU est l'hypoténuse alors que l'on nous donne sa dimension?
mais on te dit que le triangle est rectangle en T donc SU est bien l'hypoténuse et c'est bien pour cela que tu ne peux pas tracer le triangle sans faire une construction , ce que j'ai essayé de t'expliquer ce matin.
je ne comprends pas pourquoi tu me parles du triangle STU alors que je dois trouve le centre est le rayon du triangle UTH
SU²=TS²+TU²
8,5²=4²+TU²
72,25=16+TU²
TU²=72,25-16
TU²=56,25
TU = V56,25=7,5
la longueur de TU vaut 7,5 cm
juste ne dernière question STP après je ne t'embete plus. lorsque j'ai répondu plus haut :
le cercle circonscrit a pour centre le point 0 milieu de l'hypoténuse [TU] c'est faut alors car par rapport à mon dessin le segment TU n'est pas le milieu du cercle