Inscription / Connexion Nouveau Sujet
ellipse
Bonjour,
Je cherche à écrire l'équation d'une ellipse de demi-grand axe a parallèle à x, de petit axe b parallèle à y et de centre (x0,y0).
Je dirais (x-x0)²/a² + (y-y0)²/b² = ?
Je ne parviens pas à écrire le terme à droite de l'égalité.
Sur wikipédia, je trouve 1 mais je ne comprends pas pourquoi.
Pouvez-m'aider ?
Merci d'avance
bonjour
ben c'est l'équation d'une ellipse... que veux-tu de plus ?
une équation paramétrique est :
x = x0 + a cos(t)
y = y0 + b sin(t)
salut
mais si tu veux tu peux mettre n'importe quel réel strictement positif k ...
et il sera toujours possible de revenir à 1 ... (mais la longueur de tes axes ne seront plus les valeurs initiales ...
Je suis intéréssé par les réponses, je rentrais juste chez moi.
C'est que je me suis dit l'équation d'un cercle est (x-x0)^2 +(y-y0)^2 = r^2
Alors pour une ellipse je voudrais remplacer r^2 par quelque chose mais je ne sais pas quoi.
Et comme par habitude, je sais que la partie x est divisée par a^2 et celle de y par b^2, je l'ai mis sous cette forme.
Pourquoi peut-on mettre quel nombre positif ? J'ai compris pour positif parce qu'un distance est positive mais pourquoi peut-on choisir n'importe quel nombre s'il est positif, cela ne devrait pas être un nombre bien définie ?
pour répondre à ton problème précis, c'est ...=1
mais faudrait savoir ce qu'est la définition d'une ellipse avant de parler d'équation.
D'accord, d'après mes connaissances, une ellipse est un cercle applatit.
Il faut donc partir de mes connaissances sur les cercles.
Pour déterminer l'équarion d'une figure, il faut connaitre sa/ses caractéristique(s), ici: la coordonné de son centre et son rayon puis on place les variables par rapport au repère créé (est-ce que le raisonnement est correct ?)
Il faut donc trouver une relation liant x, x0, y, y0 et r.
On se place sur une point quelconque du cercle et d'après le théorème de Pythagore on peut écrire:
L'équation d'un cercle de rayon r et de centre (x0,y0) est (x-x0)2 + (y-y0)^2 = r2
Mais aussi on peut utiliser un système équation paramétrique: (t étant l'angle que forme le segment de l'origine au point quelconque avec l'horizontale)
{x=x0+r cos t
{y=y0+r sin t
Par ma connaissance qu'une ellipse est un cercle applatit, je voudrais son équation.
J'effectue alors le même raisonnement que précédemment: je cherche une relation liant x xo y yo a et b:
D'après wikipédia:
((x-x0)/a)2 + (y-y0)/b)2 = 1
Revenons au cercle: a=b=r donc je trouve bien la même équation que précédemment.
Mais je n'arrive pas à trouver le raisonnement pour pouvoir marquer cette équation
Pour être clair, quand je place un point quelconque sur l'ellipse, je créé un triangle rectangle donc les deux côtés touchant l'angle droit sont x-x0 et y-y0 et j'aimerai bien exprimée si c'est possible l'hypothénuse en fonction de a et de b mais je n'y arrive pas
Ton ellipse est l'image par une affinité de d'un cercle. Avec des mots : tu prends le cercle de rayon a, tu ne touches pas sur l'axe des abscisses, mais tu le compresses en ordonnées d'un facteur b/a.
C'est à dire que l'ellipse (de centre 0) de demi-grand/petit axes a et b est
en utilisant la paramétrisation habituelle du cercle
.
Si (u,v) est un point de E, il vérifie u²/a² + b²/a² = 1.
Réciproquement, si (u,v) est un couple de réels tels que u²/a²+v²/b² = 1, alors (ub)²+(va)² = (ab)². Donc et donc il existe un angle
tel que
et
. Donc
.
Il faut aussi traiter les cas dégénérés ou a et b peuvent être nuls, mais àa tu dois savoir le faire sans problème normalement 
en fait, il y a plusieurs définitions historiques de l'ellipse, évidemment équivalentes.
La notion d'équation n'est venue que bien plus tard dans l'histoire des sciences.
définition 1 (historique) : un cas particulier de l'ensemble des coniques : intersection d'un cône avec un plan (parabole / hyperbole / ellipse)
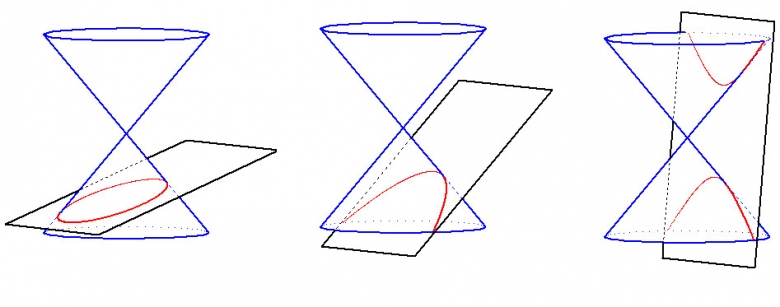
c'est aussi l'intersection d'un cylindre avec un plan non parallèle à l'axe.
définition 2 (usuelle) : : étant donné un réel e>0, une droite D et un point F n'appartenant pas à D une conique est l'ensemble des points M tels que MF = e d(M,D)
F s'appelle un foyer et D la directrice associée au foyer F
l'ellipse est le cas particulier où 0 < e < 1
mise en équation : (dans le cas de l'ellipse)
en prenant le repère(F,i,j) orthonormé tel que D a pour équation x=d
MF² = e² d(M,D)² donne :
x² + y² = e² (x-d)²
après calcul (un peu lourdingues), regroupement, mise sous forme canonique des carrés, on obtient :
avec
ce qui donne le centre (x0 ; 0} dans ce repère et ses paramètres (petit et grand axe)
un système d'équations paramétriques s'en déduit avec du cosinus et du sinus vu qu'on a deux nombres dont la somme des carrés vaut 1
ce que dit Ulmiere est une conséquence de cela...
une fois l'équation obtenue, on montre qu'il y a une autre foyer F', symétrique de F par rapport au centre de l'ellipse, associé à une autre directrice (symétrique de D).
on montre aussi que l'ellipse est l'ensemble des points tels que la somme des distances aux foyers (F et F') est constante (définition bifocale). Ce qui permet de la tracer par la méthode du jardinier
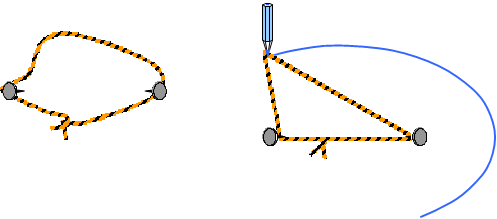
on montre aussi une propriété mirifique de l'ellipse : la tangente en M est bissectrice extérieure de l'angle (MF ; MF')... ce qui veut dire que dans billard elliptique, si 2 billes sont placées aux foyers, on peut en frapper une (sans effet) dans n'importe quelle direction, elle ira, après une bande, choquer l'autre.
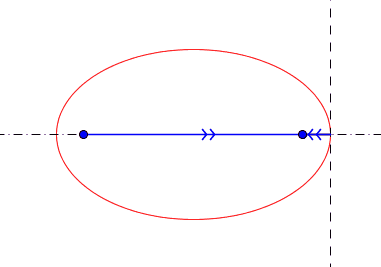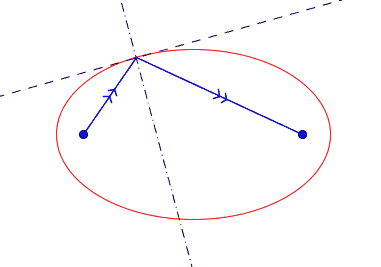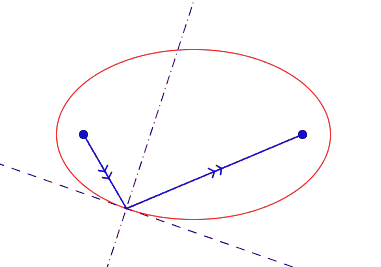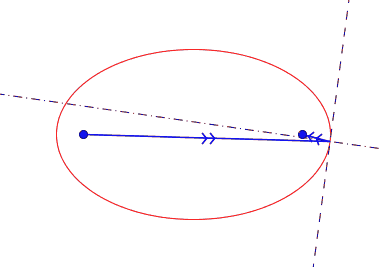
en fait ce qu'on appelle la "définition bifocale" est plutôt une conséquence de la définition géométrique historique...
mais bon, comme souvent en math on peut permuter les notions de "définition" et de "propriétés" qui en découlent
Bonjour
pour "retrouver" la valeur de 1, loshleo aurait pu se poser la question des points "extrêmes" : si on veut les demi axes indiqués, on doit avoir les points (x_0+a; y_0) et (x_0; y_0+b) sur l'ellipse
en remplaçant dans son début d'équation, il aurait retrouvé son 1
La propriété "mirifique" de l'ellipse est celle qui fait que dans les stations de métro parisiennes, on entend distinctement quelqu'un qui parle sans hausser le ton sur le quai d'en face, si on est (et le quidam aussi ) au bon endroit du quai
C'est aussi celle qui permet de griller une saucisse de tous les côté avec une seule résistance chauffante et sans faire tourner la saucisse 
lafol
exact. d'ailleurs cela m'est arrivé de subie l'expérience du métro alors que j'étais seul sur un quai au point focal et d'entendre deux personnes qui parlaient sur le quai opposé pile poil à l'autre point focal... comme si elles me chuchotaient à l'oreille ! l'effet est surprenant.
cette propriété est connue depuis longtemps et a même été utilisée pour confesser des pestiférés en évitant tout contact physique :
il me semble que ça a été utilisé dans un film d'espionnage, aussi, mais alors me rappeler lequel ...
j'ai aussi pu vérifier personnellement, une fois où un poivrot grommelait en face, je ne sais plus quelle réflexion j'ai faite mezzo voce à son sujet à mon voisin, le bougre a tout entendu comme si je lui avais chuchoté à l'oreille ! il s'est mis dans une rage !






