Inscription / Connexion Nouveau Sujet
Enigmo 294 : Les nombres "iso-décimalo-puissant"
Bonjour tout le monde,
on dira qu'un nombre entier positif P est iso-décimalo-puissant s'il existe un nombre entier positif N qui, mis à la puissance P, possède exactement P chiffres.
Par exemple, le nombre 2 est iso-décimalo-puissant car 9^2 = 81 possède 2 chiffres.
De même, 3 est iso-décimalo-puissant car par exemple 5^3 = 125 possède 3 chiffres.
En d'autres termes, s'il existe un entier positif N tel que N^P possède P chiffres alors P est iso-décimalo-puissant.
Question : Quel est le plus grand nombre iso-décimalo-puissant ?
Pour la réponse, vous donnerez P, ainsi que N tel que N^P possède P chiffres.
S'il existe plusieurs solutions, vous n'en donnerez qu'une seule.
Par contre, si vous pensez que le nombre 3 donné en exemple est le plus grand, alors vous répondrez que 3 est le maximum.
Bonne recherche ! 
PS (12H10) : je corrige 5^3 = 125 et non pas 123 !
 salut,
salut,
le plus grand nombre est 21.
En effet, 9 puissance 21 possede 21 chiffres.
9^21=109418989131512359209
 Bonjour,
Bonjour,
Le plus grand nombre iso-décimalo-puissant est p=21
Avec n=9, on a n^p = 109418989131512359209
Merci pour cette énigme bien trouvée !
 le plus grand nombre iso-décimalo-puissant est 21
le plus grand nombre iso-décimalo-puissant est 21
car 9^21=109 418 989 131 512 359 309
composé de 21 chiffres
 Bonjour jamo
Bonjour jamo 
Hum, ça sent le poisson, mais j'ai beau relire l'énoncé, je ne vois pas d'autre réponse que .
, un nombre de 21 chiffres décimaux.
(décimalo, ça veut bien dire en base 10, hein ? 5^3 = 123 c'est juste une coquille, c'est faux dans n'importe quelle base, hein ?)
Bon, peut-être que juste après avoir appuyé sur "poster", j'y verrai plus clair 
J'hésite, j'hésite...
Bon allez, j'me lance !
Merci pour l'enigmo.
 Bonjour Jamo,
Bonjour Jamo,
Le plus grand nombre iso-décimalo-puissant est 21.
P=21,N=9,N^P=109 418 989 131 512 359 209 qui possède 21 chiffres.
Merci pour l'énigmo. 
 Bonjour jamo, bonjour à tous,
Bonjour jamo, bonjour à tous,
921 a 21 chiffres
Mais pour p>21, 9p a p-1 chiffres et 10p en a p+1. Merci à mon tableur... 
Ma réponse est donc 21.
 Bonjour
Bonjour
p est forcement inferieur a 10 puisque 10puissance n a n+1 chiffres quel que soit n
le calcul des puissances de p par excel donne que jusqu'a 21, 9puissancen possede n chiffres et que au del de 21, il y en a moins de n
donc pour moi
21 est le plus grand nombre iso-décimalo-puissant avec 921 qui possede 21 chiffres
vous donnerez P, ainsi que N tel que N^P possède P chiffres
 Bonjour
Bonjour
vous donnerez P, ainsi que N tel que N^P possède P chiffres.
P = 21 et N = 9
| 9^21 = 1.094189891·10^20 = 984770902100000000000 qui possède 21 chiffres
A+
 Bonjour,
Bonjour,
Le plus grand nombre IDP est P=21, car pour N=9 : 921 comporte 21 chiffres.
Explication :
10p comprend toujours p+1 chiffres. Donc N est au plus égal à 9.
Pour avoir P chiffres, NP doit pouvoir s'écrire : NP = U.10P avec : 0,1 < U < 1
Et dans ce cas, U = (N/10)P (<1 et décroissante).
Pour U*=0,1 on trouve : P* = 1/(1 - Log10(9)) ~ 21,85
Donc 21 convient, mais pas 22.
 P=21 9^21 possède 21 chiffres 9^21=109 418 989 131 512 359 209
P=21 9^21 possède 21 chiffres 9^21=109 418 989 131 512 359 209
donc au mieux N=9 et P 21.8543453268
21.8543453268
Il reste à tester 9^21= 109 418 989 131 512 359 209 (calculatrice windows ou xcas ![]() [lien] ou …)
[lien] ou …)
 Bonjour et merci à Jamo.
Bonjour et merci à Jamo.
Je dirais que le plus grand nombre machintruc est
21.
Pour N=9, N^21 a 21 chiffres.
(on voit facilement que N ne peut pas dépasser 9)
 Bonjour,
Bonjour,
p = 21 avec N = 9
921 = 1 09418 98913 15123 59209
j'ai cherché N et p avec p-1  log(Np) < p .
log(Np) < p .
Ce qui donne 1 - 1/p  log N < 1 .
log N < 1 .
log N < 1 donne N < 10 .
1 - 1/p  log N donne p
log N donne p  1/(1-logN)
1/(1-logN)
1/(1-logN) est le plus grand pour N = 9 ; on a alors 1/(1-logN)  21,8 . D'où le pus grand p qui est 21 .
21,8 . D'où le pus grand p qui est 21 .
 Bonjour
Bonjour
Je pense que le plus grand entier iso-décimalo-puissant est P = 21.
En effet, à partir de P=22, il y a un "trou" entre 9^P qui compte P-1 chiffres (ou moins), et 10^P qui en compte P+1.
Merci pour ce bel énigmo, et à bientôt !
 Bonjour et merci beaucoup pour l'énigme !
Bonjour et merci beaucoup pour l'énigme ! 
Je pense que le plus grand nombre iso-décimalo-puissant est 21.
À bientôt !
 Bonjour,
Bonjour,
Merci pour cette énigme.
P=21 N=9 et 921=109 418 989 131 512 359 209 (21 chiffres)
PS: dans le cas de cette énigme, je ne vois pas comment il pourrait exister plusieurs solutions à l'énigme...
Donc la ligne habituelle "S'il existe plusieurs solutions, vous n'en donnerez qu'une seule." n'a peut être pas lieu de figurer dans l'énoncé 
 Bonjour !
Bonjour !
On veut trouver le plus grand P tel que
E(log(N^P))+1=P donc E(P log(N))+1=P donc comme x-1 < E(x) <= x, on a
P <= 1/(1-log N) et N <= 9 (cas N=10 absurde) d'où P <= 21.
Or E(21 log 9) + 1 = 21 donc P=21 et N=9.
Confirmation Maple :
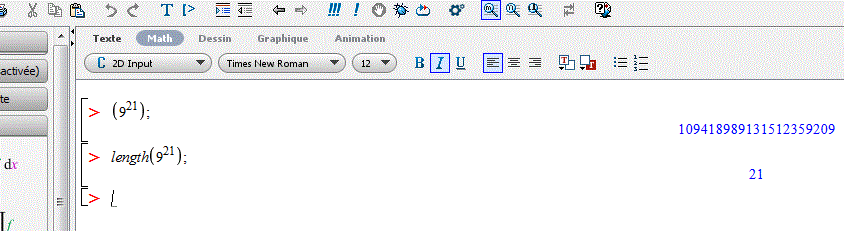
 Bonjour,
Bonjour,
Je trouve 21. 921 = 109418989131512359209
Mon raisonnement est le suivant :
10P comporte P + 1 chiffres. Donc le plus grand N possible est 9. Si 9P n'a que P -1 chiffres, P ne peut pas être iso-décimalo-puissant. J'ai donc calculé les puissances de 9 jusqu'à 922, la première qui donnait un nombre de taille P - 1.
Merci pour l'énigme. 
 Voici ma démarche.
Voici ma démarche.
D'abord, quelques tests "à la main" et hypothèses
Notation : on appellera les nombres iso-décimalo-puissants d'un rang n tous les np dont le nombre de chiffres est égal à p.
On sait que , ainsi 0 n'est pas un nombre iso-décimalo-puissant. Donc un nombre iso-décimalo-puissant est strictement positif.
Donc par la suite, et
.
donc le rang 0 ne possède aucun nombre iso-décimalo-puissant car un nombre ne peut pas avoir 0 chiffre.
donc le rang 1 ne possède qu'un seul nombre iso-décimalo-puissant : 1 (
).
Donc le rang 2 semble ne posséder aucun nombre iso-décimalo-puissant.
Donc le rang 3 semble ne posséder qu'un seul nombre iso-décimalo-puissant : 1.
Donc le rang 4 semble posséder 2 nombres iso-décimalo-puissants : 1 et 2.
On s'arrête là.
On peut émettre une conjecture : si le plus grand nombre iso-décimalo-puissant d'un rang n est p, alors le rang n possède p nombres iso-décimalo-puissants qui sont par conséquent : p; p-1; p-2; ...; 1.
Par exemple, 2 est le plus grand nombre iso-décimalo-puissant du rang 4. Donc ce dernier possède 2 nombres iso-décimalo-puissants : 1 et 2.
Un autre exemple : 6 est le plus grand nombre iso-décimalo-puissant du rang 7, donc ce dernier possède 6 nombres iso-décimalo-puissants : 1, 2, 3, 4, 5 et 6.
En supposant que la conjecture est vraie, alors il est possible de créer un algorithme simple.
Création de l'algorithme, étape par étape
Avant tout, on va forcément avoir besoin d'une fonction permettant de calculer le nombre de chiffres d'un nombre x.
On introduit une variable qui va compter les chiffres de x. Sa valeur initiale est 1.
On divise x par 10. Si le résultat est supérieur ou égal à 1, alors on incrémente le compteur de 1 et on recommence.
Essayons avec 732 :
732/10 = 73,2  1 ; compteur = 2.
1 ; compteur = 2.
73,2/10 = 7,32  1 ; compteur = 3.
1 ; compteur = 3.
7,32/10 = 0,732 < 1 : la boucle s'arrête et le compteur est finalement égal à 3, qui est bien le nombre de chiffres de 732.
Plus qu'à coder. En Python, cela donnerait quelque chose comme :
def nbrchiffres(x):
compteur = 0
while x >= 1:
x /= 10
compteur += 1
return compteur
Parlons de l'organisation de l'algorithme en lui-même. L'idée, c'est de trouver tous les i.d.p du rang 1, puis du rang 2 etc. et ainsi, on sera sûr d'avoir une liste exhaustive.
Avant de déterminer le cas général, intéressons-nous par exemple au rang 7.
On teste 71, puis 72 etc. jusqu'à ce qu'on tombe sur un nombre p tel que 7p ne possède pas le même nombre de chiffres que p. Alors, en utilisant la conjecture, et bien c'est bon, on aura déterminé tous les i.d.p du rang 7.
Comment on code ça ? D'abord, introduisons la puissance p, qui est d'abord égal à 1. Ensuite on fait 7p. Grâce à la fonction qu'on a codé auparavant, on calcule le nombre de chiffres de 7p. Si ce nombre est égal à p, alors parfait, p sera un i.d.p de rang 7. Dans ce cas, on recommence, et bien sûr en incrémentant p de 1. Et ainsi de suite jusqu'à ce que la condition ne soit plus respectée.
Voici un codage possible :
import math
n = 7
p = compteur = 0
nbrIDP = 0
while compteur == p:
p += 1
x = pow(n, p)
compteur = nbrchiffres(x)
if compteur == p:
nbrIDP += 1
print("Le rang",n ,"possède",nbrIDP, "nombre(s) iso-décimalo-puissants.")
Et voici la sortie :
Le rang 7 possède 6 nombre(s) iso-décimalo-puissants.
Et on peut vérifier à la calculatrice :
 7 chiffres.
7 chiffres.
Bon, maintenant on va coder le cas général, sous forme de fonction pour que ce soit plus pratique à introduire dans notre programme global (il faudra penser à introduire le module "math" au début) :
def nbrIDPrang(n):
p = compteur = 0
nbrIDP = 0
while compteur == p:
p += 1
x = pow(n, p)
compteur = nbrchiffres(x)
if compteur == p:
nbrIDP += 1
return nbrIDP
Bon. C'est bien beau, mais ça ne répond toujours pas à l'énigme. Donc comment va-t-on s'y prendre ? C'est simple : on va déterminer le nombre de i.d.p de tous les rangs et du même coup déterminer l'i.d.p le plus grand, répondant ainsi à l'énigme. "Tous" n'est pas précis : on ne peut évidemment pas le faire pour tous les rangs (il y en a une infinité), mais on pourra le faire pour un très grand nombre de rangs, on sera donc pratiquement certain de la réponse.
Autre chose : on ne va afficher que les rangs dont le nombre d'i.d.p est supérieur au nombre d'i.d.p maximum. Cela permet de filtrer, ainsi on obtiendra des résultats de plus en plus grand.
Par exemple : supposons que le nbr d'i.d.p du rang 8 est 4, alors le maximum est 4 et on l'affiche. Ensuite on va tester le nbr d'i.d.p de 9, supposons que c'est 3. Oui, mais 3<max=4, donc on ne l'affiche pas. Ensuite on teste le nbr d'i.d.p de 10, supposons que c'est 6. Or 6>max=4, donc on l'affiche. Et ainsi de suite.
Donc au départ, n = 1. On compte le nombre d'i.d.p de 1, puis de 2, de 3 etc. et en pensant à ne garder que les valeurs de plus en plus grandes !
Voici donc le code final :
import math
def nbrchiffres(x):
compteur = 0
while x >= 1:
x /= 10
compteur += 1
return compteur
def nbrIDPrang(n):
p = compteur = 0
nbrIDP = 0
while compteur == p:
p += 1
x = pow(n, p)
compteur = nbrchiffres(x)
if compteur == p:
nbrIDP += 1
return nbrIDP
boucle = n = 1
maximum = 0
while boucle == 1:
nbrIDP = nbrIDPrang(n)
if nbrIDP > maximum:
print("Le rang",n ,"possède",nbrIDP, "nombre(s) iso-décimalo-puissants.")
maximum = nbrIDP
n += 1
Et la sortie tant attendue :
Le rang 1 possède 1 nombre(s) iso-décimalo-puissants.
Le rang 4 possède 2 nombre(s) iso-décimalo-puissants.
Le rang 5 possède 3 nombre(s) iso-décimalo-puissants.
Le rang 6 possède 4 nombre(s) iso-décimalo-puissants.
Le rang 7 possède 6 nombre(s) iso-décimalo-puissants.
Le rang 8 possède 10 nombre(s) iso-décimalo-puissants.
Le rang 9 possède 21 nombre(s) iso-décimalo-puissants.
La réponse probable à l'énigme est donc 21. On vérifie :
En conclusion, on peut dire que ma méthode a 2 défauts, qui font que je ne suis pas complètement certain de ma réponse : le premier, et le plus gros, c'est que ma méthode suppose que la conjecture que j'ai émise est vraie, or je ne l'ai pas prouvé. Le deuxième, c'est qu'il est impossible de tester tous les rangs possibles, ce qui laisse donc une place au doute. Mais ce dernier est cependant infime : à l'heure où j'écris ces lignes, cela fait maintenant plusieurs heures que mon programme tourne et qu'il reste bloqué sur le rang 9. Je ne sais pas combien de rangs il a testé jusqu'alors mais ça doit être absolument colossal, c'est pourquoi je serais très étonné si ma réponse s'avère être fausse pour cette raison.
Bien, j'ai fini mon blabla, je me suis bien amusé !

À bientôt !
 En fait, je me suis franchement embêté pour rien.
En fait, je me suis franchement embêté pour rien.
Si n 10, alors le nombre n1 possède au moins 2 chiffres et non 1. Ainsi, le rang n ne possède pas de nombre(s) i.d.p.
10, alors le nombre n1 possède au moins 2 chiffres et non 1. Ainsi, le rang n ne possède pas de nombre(s) i.d.p.
Donc aucun rang supérieur ou égal à 10 ne possède de nombres i.d.p.
Il ne faut donc considérer que les rangs n entre 1 et 9, ce qui me conforte encore plus quant à l'exactitude de ma réponse.
Cependant, cela repose encore une fois sur ma conjecture. Si celle-ci s'avère fausse, alors j'ai faux de A à Z.
 Bonjour,
Bonjour,
Il s'agit de 21.
En effet, si a k chiffres, alors n<10
qui a k+1 chiffres.
De plus tous les nombres jusqu'à 21 sont iso-décimalo-puissants.
Mais si
qui a moins de k chiffres.
On peut le démontrer avec une simple récurrence.
Si k=22 la propriété est vraie.
Soit tel que 9^p a strictement moins de p chiffres.
Donc a moins de p+1 chiffres.
La propriété est initialisée et héréditaire.
On en déduit que le plus grand entier iso décimalo puissant est 21.
 Bonsoir,
Bonsoir,
il semblerait que ce ne soit pas très compliqué.
Inutile de tester les valeurs de N>9 car 10^P possède déjà P+1 décimales,
donc on cherche juste à tester les petites valeurs de P jusqu'à ce que 9^P ne suffise plus (i.e. 9^P possède P-1 décimales, d'où un saut de la décimale cherchée... euh pour moi c'est clair !)
Je trouve P=21 avec une unique solution pour N=9 (9^21=109418989131512359209).
Merci pour l'énigme.
 Bonjour,
Bonjour,
pour moi, le plus grand est 21.
on a 921 = 109418989131512359209 qui a 21 chiffres.
merci pour cette énigme.
 Bonjour à tous.
Bonjour à tous.
Ma réponse : P=21, N=9, 9^21 = 109418989131512359209, qui comporte 21 chiffres.
Merci pour l'énigme
 Bonjour Jamo,
Bonjour Jamo,
Le plus grand entier P vérifiant P-1  log10(NP) < P pour N
log10(NP) < P pour N
 , soit 1-1/P
, soit 1-1/P  log10N < 1 , est : P = 21 , pour N = 9
log10N < 1 , est : P = 21 , pour N = 9
921 = 109 418 989 131 512 359 209 a 21 chiffres.
 21 est le plus grand nombre iso decimalo puissant car 9^21 et 9^22 possèdent 21 chiffres, donc pour tout P > 21, 9^P possède moins de p chiffres.
21 est le plus grand nombre iso decimalo puissant car 9^21 et 9^22 possèdent 21 chiffres, donc pour tout P > 21, 9^P possède moins de p chiffres.
Comme 10^b possède b+1 chiffres, on sait que N < 10.
Si N^P possède P chiffres et si N < 9, alors 9^P possède au moins P chiffres, donc P < 22
 Bonjour,
Bonjour,
soit n,p deux entiers naturels non nuls,
on tente de déterminer la plus grande valeur de p>=3 telle que n^p comporte p chiffres.
On démontre facilement que le nombre de chiffres que contient un nombre positif x vaut E(log x)+1.
On cherche donc les nombres p, n tel que E(p log n) + 1 - p = 0
D après l encadrement p-1 <= p log n < p, on décrit n pour les valeurs allant de 5 à 9 incluses.
La plus grande valeur de p est donc 21, en effet :
9^21 = 1,09419.10^20 et contient 21 chiffres.
Merci pour l'énigme !
 Bonjour,
Bonjour,
Le nombre de chiffres de n est donné par  :
: 

 (en base 10 naturellement).
(en base 10 naturellement).
n  E(log(n)) + 1
E(log(n)) + 1
On a  (10p) = p + 1
(10p) = p + 1
On a  (9p)
(9p)  p
p
et  (9p) < p
(9p) < p 
 n < 9
n < 9  (np) < p
(np) < p
 étant strictement croissante.
étant strictement croissante.
Donc P est iso-décimalo-puissant 
 (9P) = P.
(9P) = P.
Un petit programme et on trouve max {P
 |P iso-décimalo-puissant} = 21
|P iso-décimalo-puissant} = 21
En effet  (921)=21
(921)=21
et  (922)=21
(922)=21
 Bonjour,
Bonjour,
Et voilà, mes espoirs de faire un sans-faute ce mois-ci sont anéantis.
En relisant la consigne il y a une minute, j'ai lu avec horreur :
Pour la réponse, vous donnerez P, ainsi que N tel que N^P possède P chiffres.
Je me rends compte que j'ai complètement oublié de donner N dans ma réponse.
Bien que dans le message suivant (où j'expliquais ma démarche) j'ai précisé que N = 9, et bien évidemment c'était trop tard.
C'est vraiment trop bête.

LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
LIS LA CONSIGNE EN ENTIER.
 Bonjour,
Bonjour,
Les nombres iso-décimalo-puissants sont les entiers de 1 à 21.
Le plus grand est 21, et on a :
9^21 = 1.0942e+20 qui possède bien 21 chiffres.
 Bonjour Jamo, bonjour tous!
Bonjour Jamo, bonjour tous!
Je propose 21, que 9 rend iso-décimalo-puissant, car 9^21=109418989131512359209.
En effet, aucun nombre supérieur ou égal à 10 ne peut en rendre un autre iso-décimalo-puissant (rendre un nombre P puissant, c'est être un N tel que N^P ait P chiffres). 9 s'impose alors vite comme le meilleur N à choisir pour trouver un P optimal... Après, c'est du calcul.
Merci encore!
Clôture de l'énigme
Bravo à tous ceux qui ont trouvé, j'avais pensé que ce serait plus difficile que ça ! 
Nombre de participations : 0
Temps de réponse moyen : 75:13:08.

 101
101 comment ai-je pu mettre 101 au lieu de 1020...
comment ai-je pu mettre 101 au lieu de 1020...
