bonjour Laurierie

x²+y²=1

u = 1+(x+iy)+(x²-y²+2ixy) = 1+x+x²-y²+iy(1+2x) = 2+x+i(1+2x)V(1-x²)

u = X + iY
X = 2+x => x = 2-X
Y = (3-2X)V(1-4+4X-X²)

Y = (3-2X)V(-X²+4X-3)

A vérifier...

Bonjour,

et en passant par z = cos(a)+i*sin(a)

je crois qu'on trouve :

u = [1+cos(a)+cos(2a)] +i [sin(a)+sin(2a)]

...

Et si je ne me suis pas trompé, cela donne plutot ceci :

Bonjour, je ne crois pas que l'on puisse remplacer y par la racine, car la relation y²+x²=1 donne deux solutions pour y. je vais examiner le reste merci

Je n'avais pas pensé a voir la chose comme ca et a se ramener a une courbe paramétrée! Merci!

Oui, ça revient à une courbe paramétrée avec le réel a sur [-PI ; PI].

Mais vérifie quand même ce que j'ai fait ...

tu as déjà u = (1+2cos())*e⁽ⁱ⁾

t'as direct l'équation polaire mais bon tu peux faire en carthésiennes si tu prèfères

r() = 1+2cos()

une belle fausse cardioide comme jamo a dessiné

oops

J'ai fait une erreur en remplaçant y² par 1-x²

sinon, en paramétriques X(t);Y(t)

X = 2t²+t
Y = (plus ou moins)(1+2t)Racine(1-t²)

ce qui fournit :

Bien vu jiju33, j'avais pensé aussi à mettre u sous la forme

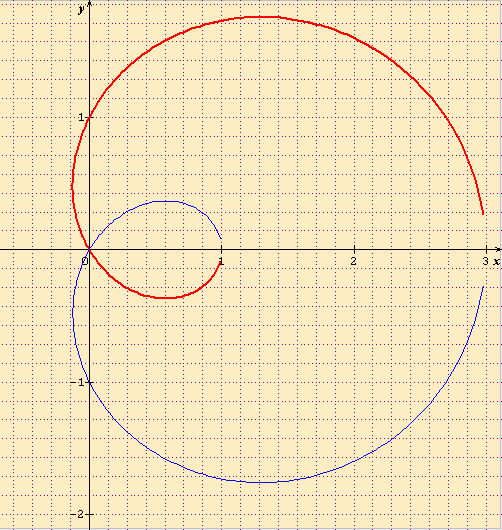
Merci pour toute vos réponses. Jiju 33 , je n'avais pas pensé a me ramener en une courbe en polaire.

Merci

Et comment s'appelle cette courbe ?

Je ne la trouve pas ici :

je propose une cardioide bouclée ^^

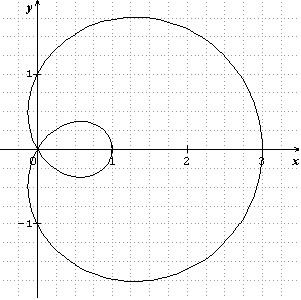
Et celle-ci, vous la connaissiez : Courbe paramétrée

J'ai trouvé !!

C'est un limaçon trisecteur !! :

sympa ton lien, jamo

Joli!

merci Laurierie

c'est issu du très bon site de Robert FERRÉOL, mathcurve, ici, en cliquant sur la maison