Inscription / Connexion Nouveau Sujet
Equation cône de révolution spé
Bonjour à tous et à toutes!
Je vous appelle à l'aide car j'ai un gros problème si quelqu'un peut m'aider je serais très contente...
Merci d'avance pour votre aide.
Le sujet du problème commence par:
"Donner l'équation du cône de révolution de sommet S(1;-1;2) dont l'axe est parallèle à l'axe (O;
) et contenant le point K(0;-1;2)". Merci...
Suicune 
Bonjour
l'axe du cône est parallèle à l'axe (O;) et son sommet S a pour coordonnées (1 ; -1 ; 2).
S est donc l'unique point du cône de cote 2.
Le cône contient le point K(0 ; -1 ; 2) ???
Il doit y avoir une erreur d'énoncé.
Exact tu as raison,je suis désolée pour cette faute de frappe la côte du point K est -2. d'où les coordonnées de K sont: K(0;-1;-2)
Voilà la rectification...Mais je n'arrive pas à cerner ton raisonnement.?.?.?. Peux tu explicitement expliquer s'il te plaît? Merci
Suicune
L'axe du cône a pour équation :
et
.
Soit un point de
,
.
on a :
La droite perce le plan
en
.
et
sont colinéaires donc il existe un réel
tel que
ainsi,
De ceci, on peut tirer
Dans le plan ,
appartient au cercle de centre le point de coordonnées
et de rayon
:
Ainsi,
c'est-à-dire :
Tout est à bien vérifier.
_____________________
Je suis nul en maths.
Merci aux bonnes volontés qui voudraient corriger
_____________________
Je suis nul en maths.
Hello,
À partir d'une autre méthode je trouve l'équation suivante :
soit
N'aurais-tu pas oublié une racine quelque part N_comme_Nul ?
Sinon ça veut dire que j'ai faux mais nos résultats sont tout de même très proche donc...
À vérifier
PS: si j'ai le temps et si nécessaire je pourrai éventuellement détailler mon raisonnement.
Bonsoir SquaL !
J'ai refais mes calculs ... et je retombe sur le même résultat 
Je suis intéressé par ton autre méthode. Si tu pouvais la mettre (si t'as le temps 
) on pourrait comparer.
Il faut que la vérité éclate ! (
)
_____________________
Je suis nul en maths.
>N_comme_Nul
"La droite (SM) perce le plan {z=-2} en en K."
c'est faux l'intersection d'une droite et d'un plan correspond a un point (si cette droite n'est pas incluse dans ce plan)
dc lorsque M parcourt le cone C l'intersection correspond au cercle d'equation cartesienne
(x-1)^2+(y+1)^2=1 de centre I(1;-1;-2) de rayon 1
donc ta situation est un cas particulier....
M,K,S ne sont pas toujours alignés...
Oui aicko, mais cela ne change pas grand chose :
mon raisonnement, je l'ai fait avec un point dont la cote est
et les deux premières coordonnées
et
.
C'est que j'ai rendu le "variable" ... erreur de ma part
Remplacer alors "" par "
".
_____________________
Je suis nul en maths.
on a vu que le cercle qui correspond a l'intersection du plan {z=-2} avec C est un cercle de rayon 1 et qui passe par K de centre I(1;-1;-2)
considerons le cercle qui correspond a l'intersection avec le plan Z=2-z avec C de centre J(1;-1;2-z)
son equation est =
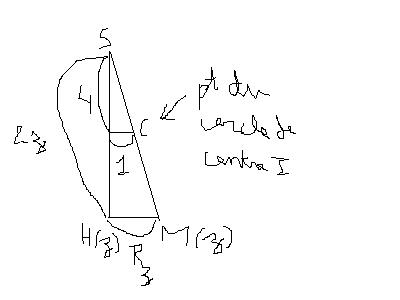
utilisons thales (voir schéma)
nous obtenons =
soit Rz=
remarque : lorsque M decrit C, nous avons z
2 donc 2-z
0 donc Rz0
ainsi l'equation de C est :
=
la solution semble correspondre a celle de N_comme_Nul
la verité a eclatée
Si ma méthode interesse la voilà..
On sait qu'un cône de centre S(1;-1;2) parallèle à l'axe Oz a une équation de la forme
De plus toute droite contenue dans le cône est une génératrice du cône (qui passe alors nécessairement par le centre).
La droite (SK) est donc une génératrice de ce cône.
On cherche alors une équation paramétrique de cette droite et on trouve
On remplace alors dans l'équation de départ, et ainsi on obtient:
d'où l'équation
À vérifier bien sur
Annuler
connectez vous