Inscription / Connexion Nouveau Sujet
Equation d'un cône
Bonjour à tous, je souhaite avoir de l'aide dans cet exercice que je n'arrive pas à résoudre.
(O;
;
;
) est un repère orthonormal de l'espace.
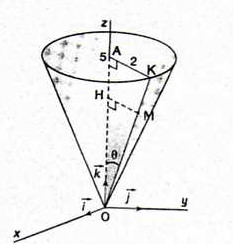
Le point A a pour coordonnées (0;0;5).
On considère le cône de révolution engendré par la rotation autour de (OA) du triangle rectangle OAK avec AK=2
1)Un point M du cône, distinct de O, se projette orthogonalement en H sur [OA].
a)Prouvez que MH/OH=2/5 puis MH²=4/25OH²
b)Traduisez l'égalité précédente à l'aide des coordonnées (x;y;z) de M.
Démontrer que si M(x;y;z) appartient au cône (y compris le sommet O) alors ses coordonnées sont données telles que:
x²+y²-4/25z²=0 et 0
z5.
2)Réciproquement, M est un point de l'espace dont les coordonnées (x;y;z) vérifient:
x²+y²-4/25z²=0 et 0z5
a) Avec les notations précédentes, démontrez que, si z
0, MH/OH=2/5
b)Déduisez-en que M est sur le cône (ne pas oublier le cas z=0)
Conclusion: Le cône a pour équation x²+ y² -4/25a²=0(avec 0z5)
3) déterminez, parmi les points suivants, ceux qui sont sur le cône:
Q(2;0;5), R(-2;1;5), S(1;1;3) et T(2;2
3;10).
4) Déterminez une équation du cône de révolution de sommet O, d'axe (O;), de base le cercle de centre B(4;0;0) et de rayon 3.
Merci d'avance...
Bonjour Mely90,
Ce problème ressemble comme presque deux gouttes d'eau à celui que nous avons commencé (et pas terminé d'ailleurs 
) hier avec le cylindre.
Question 1a : triangles semblables ou Thalès...
Le problème très semblable, mais avec un cylindre : 
Equation d'un cylindre
Voici mon devoir ! Pouvez vous le corriger s'il vous plaît et m'aider sur les points ou je n'ai pas su répondre ou mal répondu! D'avance Merci !
1.
a)D'après Thalès on a : MH/KA = OH/OA = OM/OK
KA=2 OA=5
MH x OA = KA x OH
Donc MH/OH = KA/OA = 2/5
->MH = 2/5 OH
->MH² = 4/25 OH²
b) MH = x² + y² (comme vu précédemment)
OH = racine carrée de (xH - xO)² + (yH - yO)² + (zH - zO)²
H (0 ; 0 ; z ) car H Є (Oz) et O (0 ; 0 ; 0) car O origine du repére
Ainsi OH = racine de z² et donc OH² = z
MH² = 4/25 OH²
x² + y² = 4/25 z²
x² + y² - 4/25 z² = 0
Comme [OA] hauteur du sommet et O origine du repère et sommet du cône et [OA] = 5
Si M appartient au cône x² + y² - 4/25 z² = 0 et 0<<z<<5
2.
Je n'y arrive pas puis-je avoir de l'aide ?
3.
Q (2 ; 0 ; 5) n'appartient pas au cône car x² + y² - 4/25 z² ≠ 0
R (-2 ; 1 ; 5) n'appartient pas au cône car x² + y² - 4/25 z² ≠ 0
S (1 ; 1 ; 3) n'appartient pas au cône car x² + y² - 4/25 z² ≠ 0
T (2 ; 2V3 ; 10) n'appartient pas au cône car x² + y² - 4/25 z² ≠ 0
4.
x² + y² - (3/4) (z²) = 0
Bonjour Céline030192,
Tu ne vas pas toujours "droit au but" et il y a de petites erreurs.
1a)D'après Thalès on a : MH/KA = OH/OA
tu peux en déduire immédiatement MH/OH = KA/OA = 2/5
donc
MH = OH*(2/5)
et
MH2 = OH2*(4/25)
1b) MH2 = x2 + y2
M a pour cote z et H est le pied de la perpendiculaire menée de M sur Oz, donc OH = z
Les coordonnées (x ; y ; z) d'un point M du cône vérifient donc
x2 + y2 -(4/25)z2 = 0 avec 0 z 5
2) si les coordonnées d'un point M vérifient
x2 + y2 -(4/25)z2 = 0 avec 0 z 5
ou
x2 + y2 = (4/25)z2 avec 0 z 5
pour z 0 on peut écrire
(x2 + y2) / z2 = 4/25
ou
MH2 / OH2 = 4/25
MH et OH étant des longueurs et donc des quantités positives :
MH / OH = 2/5
Tu peux en déduire que M est un point du cône
si z = 0 le point M est dans le plan de base (O,,)
x2 + y2 = 0
donc la distance de M à O est nulle et donc M est confondu avec O le sommet du cône
3) tu n'as pas bien calculé pour le point Q
La raison que tu donnes pour le point T n'est pas la bonne
4) 
Bonjour,
Tout d'abord merci pour votre raisonnement qui m'a aidé, cependant, je n'arrive toujours pas à répondre à les questions 3 et 4.
Merci d'avance
Annuler
connectez vous