Inscription / Connexion Nouveau Sujet
Equation d'un cylindre
Bonjour. J'ai un gros problème.
J'ai un devoir dont que l'on a commencé.
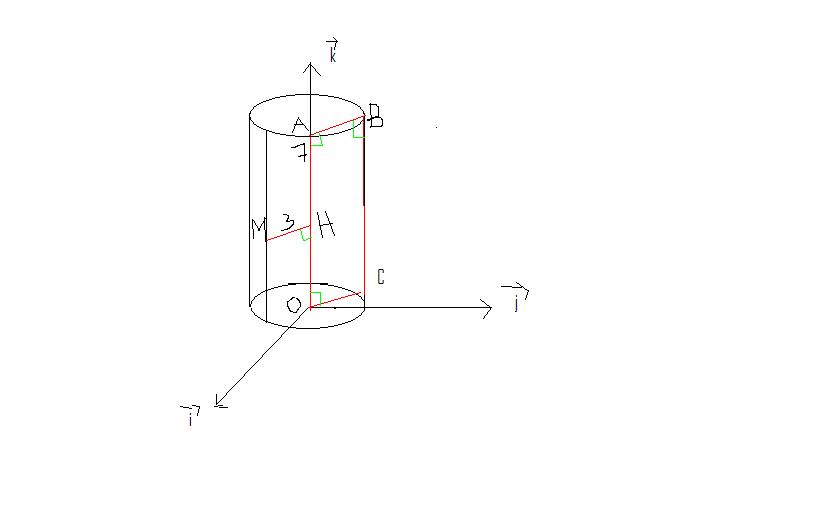
(O,i,j,k) est un repère orthonormal de l'espace. Le point A(0;0;7)
On considère le cylindre de révolution engendré par la rotation autour de (OA) du rectangle OABC avec AB = 3. Un point M du cylindre se projette orthogonalement en H sur le segment [OA] et MH = 3.
J'ai essayé de reproduire le mieux possible la figure. Excusez moi car ce n'est pas très "clair"...
1. On note(x;y;z) les coordonnées du point M. Donner les coordonnées du point H.
( j'ai pensé utiliser les coordonnées et vecteurs avec l'orthogonalité....)
Prouver que les coordonnées de M sont telles que x²+y²=9 et 0
z7 (j'ai trouvé que j'ai trouvé que M appartient à C <=> x²+y²= MH². )
2.Réciproquement, M(x;y;z) est un point de l'espace dont les coordonnées sont telles que x²+y²=9 et 0z7. Démontrer que MH=3. déduisez en que M est sur le cylindre
Conclusion: le cylindre droit a pour équation x²+y²=9 (avec 0z7)
j'ai trouvé que M appartient à C <=> x²+y²= MH².
3.Déterminer, parmi les points suivants, ceux qui sont sur le cylindre:
D(3,0,3), E(
3;6;4) et F(1,3,1)
4.Caractérisez analytiquement le cylindre d'axe (O,j) =, de bases les cercles de rayon 2, de centres respectifs O et B(0;10;0), puis le cylindre d'axe (O,
), de bases les cercles de rayon 5, de centres respectifs O et C(20,0,0).
Déjà je ne comprends pas le sens de "caractérisez analytiquement"...
5.décrivez l'ensemble des points M(x;y;z) dont les coordonnées sont telles que:
x²+y²=25 et -5z4
Merci de votre aide.
Bonjour,
Il y a un mélange entre l'énoncé et tes réponses qui ne rendent pas l'ensemble très clair.
Quelle est la première question pour laquelle tu souhaites de l'aide ?
Bonjour,
Voici la première question:
1. on note (x,y,z) les coordonnées du point M.
Donnez les coordonnées du point H
Prouvez que les coordonnées de M sont telles que x²+y²=9 et 0z7.
les coordonnées de H sont les mêmes que celles du point M
car on obtient avec les vecteurs: AM.AO =AH.AO...
Si les deux points H et M avaient les mêmes coordonnées ils seraient confondus.
Une coordonnée est la même (c'est d'ailleurs pour cela que tu as l'égalité vectorielle que tu annonces) mais les deux autres coordonnées sont différentes). Quelles sont les coordonnées d'un point quelconque de l'axe Oz ?
Pas tout à fait car on est dans l'espace à trois dimensions : donc un point quelconque de Oz a pour coordonnées (0 ; 0 ; z)
M ayant pour coordonnées (x ; y ; z) et HM étant dans un plan parallèle à xOy puisque perpendiculaire à Oz, quelles sont les coordonnées de H ? Le point H a-t-il une cote différente de M ?
Mais tu as répondu !
Puisqu'il a la même cote et que celle de M est z alors la cote de H est aussi z et donc les coordonées de H sont (0 ; 0 ; z)
2.Réciproquement, M(x;y;z) est un point de l'espace dont les coordonnées sont telles que x²+y²=9 et 0z7. Démontrer que MH=3. déduisez en que M est sur le cylindre
A quelle distance de l'axe se trouve un point qui a des coordonnées (x ; y ; z) telles que x2 + y2 = 9 ?
Où se projette sur l'axe Oz un point dont la cote vaut z tel que 0 z 7 ?
Ah d'accord tout simplement ... merci : c'est la distance de 3, et c'est le point M qui se projette sur l'axe Oz
Par définition un point est sur le cylindre si sa distance est à l'axe vaut 3 et qu'il se projette entre O et A... donc c'est un point du cylindre !
Un problème très semblable, mais avec un cône : 
Equation d'un cône
Merci a vous, j'avais le même exercice à faire et vos réponses m'ont aidé !
est une île aux trésors ! 
Je ne vois pas comment prouver que M est un point du cylindre ssi x²+y²=9
sachant que M(x;y;z) et H(0;0;3)
car je trouve HM²=x²+y²+9 
Les coordonnées de M : (x ; y ; z)
H est le pied de la perpendiculaire issue de M sur OA donc les coordonnées de H sont : (0 ; 0 ; z)
Et MH = 3
J'ai le même exercice à faire mais je ne comprends pas pourquoi on prend le carrée de MH au niveau de la premiere question ! Coll si tu te connectes sur le forum aide moi stp!
J'essaye vraiment mais je ne comprends certaines choses ! Il faut m'aider rapidement svp mais je ne veut pas les réponces je veut juste que l'on m'aide et que l'on m'explique!
Bonjour Céline,
Pour exprimer la longueur MH en connaissant les coordonnées de M et celles de H, tu calcules la distance de M à H
Pour cela, tu utilises le théorème de Pythagore et donc tu calcules MH2
Les coordonnées de M sont (x;y;z) les cordonées de H (0;0;z) donc la longueur Mh si o, calcul on trouve MH=racine carée (x²+y²) si on met au carrée les deux membres de l'équation on obtient Mn²= x²+y² -> 3²= x²+y² -> x²+y²= 9.
Est-ce la solution à la question posée (doute) ?
Oui, c'est la réponse.
Mais tu vois que tu n'as même pas besoin de prendre la racine carrée pour ensuite élever au carré...
Coordonnées de M : (x ; y ; z)
Coordonnées de H : (0 ; 0 ; z)
donc
Coordonnées de : (0-x ; 0-y ; z-z) = (-x ; -y ; 0)
Carré de la norme de ce vecteur :
MH2 = x2 + y2
et puisque MH = 3 il faut MH2 = 9
donc x2 + y2 = 9
Merci encore de bien vouloir corriger mon devoir le voici :
1.
*H (0 ; 0; z) car H Є (Oz)
*Coordonnées de M : (x ; y ; z)
Coordonnées de H : (0 ; 0 ; z)
Donc : Coordonnées de : (0-x ; 0-y ; z-z) = (-x; -y; 0)
-> MH2 = x2 + y2 -> MH = 3 il faut MH2 = 9
Ainsi : x2 + y2 = 9
M ayant pour coordonnées (x ; y; z) et (HM) étant dans un plan parallèle à (xOy) car perpendiculaire à (Oz) -> H et M ont la même côte.
zM = zH et H Є [OA] et vecteur OA (0 ; 0 ; 7) donc 0<<zH<<7 ainsi 0<<zM<<7.
Ainsi les coordonnées de Om sont telles que : x2 + y2 = 9 et 0<<zM<<7.
2.
* x2 + y2 = 9 ->x+y=3 ainsi HM=3
* H Є axe de rotation du rectangle engendrant le cylindre de révolution et HM=3. Pour que M soit sur le cylindre, il faut que HM<<3 -> HM=3 ainsi : M est sur le cylindre.
3.
* D (3 ; 0 ; 3) est sur le cylindre car : x2 + y2 = 9 et 0<<zD<<7.
E ( 3 ; 6 ;4) est sur le cylindre car : x2 + y2 = 9 et 0<<zE<<7.
F (1 ; 3 ; 1) n'est pas sur le cylindre car : x2 + y2 ≠ 9
4.
*Le cylindre d'axe (O ; j) , de bases les cercles de rayon 2, de centres respectifs O et B(0;10; 0) est caractérisé par : x² + z² = 4 avec 0<<y<<10.
Le cylindre d'axe (O,i), de bases les cercles de rayon 5, de centres respectifs O et C (20 ; 0 ; 0) est caractérisé par : y² + z² = 5 avec 0<<x<<20.
5.
* Les points M (x ; y ; z) dont les coordonnées sont telles que x² + y² = 25 et
-5<<z<<4 sont les points appartenant au cylindre d'axe (Ok), de bases les cercles de rayons 5 de centre respectifs 0 (0 ; 0 ;-5) et C(0 ;0 ; 4).
Voila mon travail ! (je n'est pas oublier mais je n'arrive pas à écrire les fléches de vecteurs sur l'ordinateur).
J'attend ta réponce ...
Question 2
Il n'est pas possible de dire que puisque x2 + y2 = 9 alors x + y = 3
D'accord pour les réponses à la question 3 (même si tu as mal recopié les coordonnées de E ; il manque les racines carrées)
Question 4 : tu as oublié d'élever au carré le rayon des bases du cylindre de rayon 5
Question 5 : oui
Ce sont de petites erreurs qu'il te sera facile de corriger. C'est bien !
Merci! J'ai réussi à corriger mes erreurs hors-mi celles de la question 2. Je ne vois pas comment faire! Encore un petit coup de pouce?
Annuler
connectez vous