Inscription / Connexion Nouveau Sujet
Équation différencielle et méthode d'Euler
Bonjour à tous,
Je me permet de solliciter votre aide pour un exercice de math sur lequel je bloque complètement car je n'ai pas encore vu ceci concrètement en cours..
Voici le sujet :
Soit une l'équation différentielle xy' = 2y + 2 avec la condition initiale y(1) = 1.
On considère une fonction f solution de cette équation différentielle.
Calculer grâce à la méthode d'Euler avec un pas de 0,5 les approximations de f(x) et f'(x).
C'est ici que je bloque car je ne vois pas comment utiliser la méthode d'Euler avec une équation de ce type..
Merci d'avance pour votre aide!
PS : veuillez excuser d'éventuelles fautes d'orthographes et/ou de présentation car je suis sur mon portable et je ne vois pas toujours clairement ce que j'écris.
Bonsoir,
On détermine une suite de points :
où
est le pas donné.
avec l' approximation affine de
au voisinage de
Or ici
donc
et avec , on obtient:
On a donc notre suite de points déterminée par:
avec

Merci beaucoup cailloux pour cette réponse des plus complètes mais j'avoue ne pas tout comprendre ... parce que les x0 et y0 trouvés à la fin correspondent à quoi concrètement ? On doit remplacer ceux de l'équation différentielle par eux ? Ou alors ils correspondent aux points de f(x) ou f'(x) ?
Désolé si je pose des questions idiotes mais je suis vraiment perdu :/
L' énoncé indique qui correspond au premier point
de la courbe avec
et
Ensuite on peut calculer de proche en proche
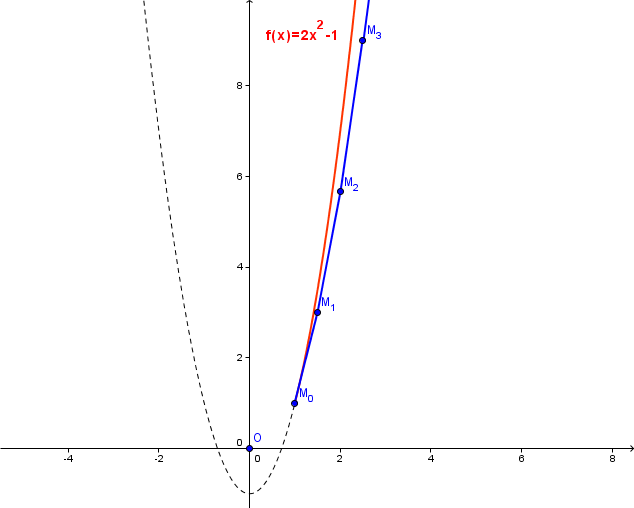
En rouge la courbe exacte solution de l' équation différentielle et en bleu l' approximation de cette solution par la méthode d' Euler:

Aaaaaaaaaah d'accooord !! En effet je n'avais pas fais le lien entre y(1) et les points mais c'est tout à fait logique ! Merci beaucoup pour cette réponse détaillée j'y vois bien plus clair maintenant ! Encore merci cailloux !!


