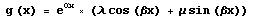Inscription / Connexion Nouveau Sujet
équation différentielle du second ordre à coefficient constant
bonjour,
je dois faire prouver ou démontrer qqch qui apparait lors de la résolution d équation différentielle linéaire du second ordre à coefficient constant (ça c'est bien un nom à rallonge)
Ex . :
a f"(x) + b f'(x) + c f(x) = 0
ar2e[/sup]rx[sup] + brerx + cerx
=> ar2 + br + c = 0
1 er cas : discrimant > 0
...
2ème cas : discriminant < 0
g(x) = ealpha x (lambda cos (beta x) + mu sin (beta x))
où alpha = - b /2a et beta = (la racine de 4ac-b2) / (2a)
ensuite mon prof de math me marque :
g'(x) = ... et g"(x)= ...
puis
a g"(x) + b g'(x) + c g = ... = 0
et il nous dit on peut montrer que ceci = 0 pour tout alpha, mu et x (si j ai bien noté)
Ma question (enfin) comment faire la démonstration, il a dit que ca prendrait au moins 3 pages, alors je pars avec ca
a g"(x) + b g'(x) + c g = ... = 0 mais apres que faire ?
bonsoir  ,
,
pour ce qui est du nom à rallonge:
la résolution d'équation différentielle linéaire du second ordre à coefficient constant
regardes ce que cela veut dire:
resoudre une équation différentielle
ton équation fait intervenir des dérivées
linéaire, signifie que tu ne trouveras pas ce genre de chose
du second ordre, permet de dire que tu as du f, f' et f"
(pas de , ou autre
 )
)
à coefficient constant signifie que:
dans af"(x)+bf'(x)+cf(x)=..
a, b et c sont indépendants de x
pour ton problème,
je n'ai pas bien compris, ce que tu demandes
en fait il faudrait que je fasse la partie des 3 petits points
a g"(x) + b g'(x) + c g = ... = 0
a mon avis il faut partir comme ca :
g(x) = ealpha x (lambda cos (beta x) + mu sin (beta x))
je dois alors calculer la dérivée première et la dérivée seconde. ensuite calculer a g"(x) + b g'(x) + c g = ... = 0
tu penses que c'est ça ? j ai pas envie de me lancer la dedans si c'est pas ca et merci pour tes explications quant au nom
c'est exactement cela 
tu dérive g pour avoir g', puis tu dérive g' pour avoir g"
après il te suffit de faire le calcul ag"(x)+b g'(x)+c g(x)
c'est un calcul long mais tu dois aboutir à 0

ok ok d'accord merci
et maintenant comment on dérive ? si y a des volontaires pour mon dur labeur...
voici l'équation à dériver :