Inscription / Connexion Nouveau Sujet
équation second degre
bonjour, j'ai ce Dm de math et je suis perdu et incapable de résoudre cet exercice
on considère l'équation du second degré ax2+bx+c=0. a,b,c sont des réels différents de 0. Dans un repère orthonormé (O;i;j) du plan, on définit les points A(a;0); B(a;b) et C(a-c;b). Soit le point P de coordonnées (-1;a), ou a est un réel quelconque et m le point d'intersection des droites (OP) et (AB)
1 Faire une figure a l'aide de Geogebra
2 Démontrer que le triangle OMC est rectangle en M si et seulement si a est solution de l'équation ax2+bx+c=0
3 Décrire une construction géométrique permettant de résoudre cette équation ax2+bx+c=0
4 résoudre géométriquement les équations suivantes :
* x2+x-1=0
* 5x2+4x+1=0
* -2x2+3x-1=0
* 4x2+5x+6=0
5 a quelle condition géométrique existe-t-il des solutions ? traduire cette condition algébriquement et retrouver la condition déjà connue
qui aurait la gentillesse et le temps de m'aider a comprendre cet exercice. Merci par avance et bonne soirée
Bonjour,
1) La figure pas trop de souci, je te laisse faire...
2) Commences par d'abord déterminer une équation de la droite (OP), puis (AB).
Puis détermines ensuite les coordonnées du point M.
Salut
Soit le point P de coordonnées (-1;a), ou a est un réel quelconque
S'agit-il du même a que celui de l'équation ax2+bx+c = 0 ?
Je te demande ça car au début de l'exercice, a est un réel différent de 0
Et dans la partie que j'ai citée, ils redéfinissent a comme un réel quelconque
Pour l'instant j'ai trouvé que M(a;-
*a)
J'ai aussi trouver que OC valait 
a2+c2+b2-2ac
, que OM valait a2+(-2) et que MC valait c2+b2+2b**a+a...De là j'ai appliqué Pythagore pour prouver que OMC était rectangle en M ssi était solution de l'équation..
!!
Je suppose qu'a la question 2), le a est aussi un...
Tu as écrit :
"2 Démontrer que le triangle OMC est rectangle en M si et seulement si a est solution de l'équation ax2+bx+c=0 "
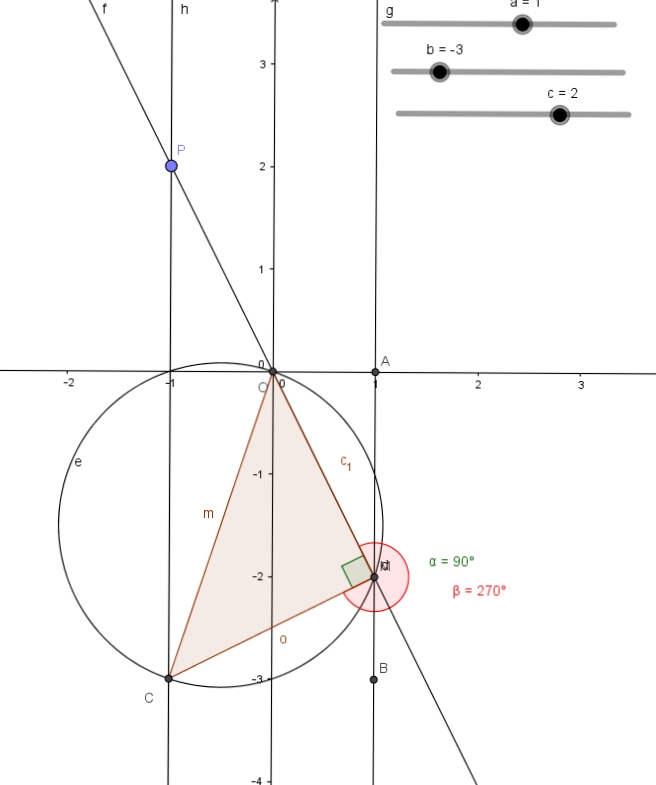
Avec la nouvelle donne, dans GEOGEBRA le point P est un point qui a toujours -12 comme abscisse donc il appartient (quel que soit à la droite "verticale d'équation ... à toi de dire ! Trace cette droite et positionne ton point P dessus.
J'ai vu que tu avais tracé un cercle. Bonne idée mais ce cercle a pour diamètre [MC].
Avant de te lancer dans les calculs, jette un œil pour voir ce qui se passe sur la figure. Prends des valeurs simples pour a b et c et résous par le calcul pour connaître les solutions de ax²+bx+c = 0.
Exple : place tes curseurs à 1, -3 et 2 (cherche les solutions x²-3x+2 = 0).
Puis tu déplaces le point P et tu regardes comment M se déplace.....
Donc, pour résoudre géométriquement ax2+bx+c, il suffit de tracer un cercle de diamètre OC et de dire que les points d'intersection de (AB) et de (C) sont solutions de l'équation?
:)
C'est un peu plus compliqué que cela...
As tu la figure complète faite avec GEOGEBRA ?
As tu essayé avec une équation simple ?
Sauf erreur, il me semble qu'il te faut déplacer le point P (-1; ) sur la droite d'équation x = -1, jusqu'à ce que le point M se positionne sur le cercle de diamètre [OC]. Lorsqu'il en est ainsi, le triangle OMC est rectangle en M et c'est l'ordonnée du point P qui est une solution de l'équation ax²+bx+ c =0 choisie.
(en général quand il y a une position de M sur le cercle, en déplaçant P à nouveau on en trouve une deuxième donc une deuxième solution pour l'équation du second degré !!)
Et pour les calculs demandés où en es tu ??
Annuler
connectez vous