si <.|.> est un produit scalaire sur E alor c'est une forme sesquilinéaire, hermitienne :

||x+y||²= <x+y|x+y>
        = <x|x> + <x|y> + <y|x> + <y|y>   //par sesquilinéarité
        = ||x||² + ||y²|| + <x|y> + conj(<x|y> )   //car hermitienne <y|x> = conj(<x|y> )
        = ||x||² + ||y||² + 2re(<x|y> )

Je ne comprend pas ta 2e question, étant donné que tu demandes d'où vient celà, mais celà est une définition, donc ca tombe de nulpart.
Dans le deuxième cas tu es dans un ev réel non?

Oui, Otto.



Tu vas là :



à la page 31 d'adobe.

Tu remarqueras que dans la partie au dessous :

Démonstration : Il n'y a qu'à l'écrire.  

Cette définition doit avoir une explication rationnelle.
Non?

Merci jiju pour ta démonstration simple et moins rébarbative que celle que l'on trouve parfois dans les manuels des "super profs de prépas agrégés depuis 15 ans".

C'est la démonstration on ne peut plus classique du résultat.

Et ça (dernière de la journée);

Comment on le démontre?, car en dvt "normal", on trouve <x|y> = 0 !!

Merci.

  

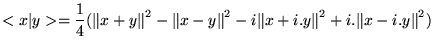
Pourquoi est ce que x|y serait 0?
Ca c'est vrai si et seulement si y et x sont orthogonaux.

Pour la derniere égalité (dite de polarisation), il suffit de développer le membre de droite.

pour la formule de derby3.une rectification il faut changer le signe pour les deux dernier termes.

Anass

Non, excuse, à vue de nez, on trouve en développant :

<x|y> = xy + ixy.

Mouais,...

Pas convaincu plus que ça.

<smiley-déçu>

Ca veut dire quoi
<x,y>=xy+ixy ?

Ca n'a aucune signification

C'est ce que donne le dvt du deuxième membre non?

Ou alors :
<x,y> = <x,y> + i <x,y>
ou encore :
      = ||xy||² + i ||xy||²

Si j'ai fait une grossière erreur, dîtes le moi, et ne me laissez pas m'enfoncer dans les crevasses des espaces préhilbertiens!


Au fait, j'ai une autre question cette fois ci se situant dans E espace préhilbertien non nécessairement finie (comme moi )

Si F est un sous-espace vectoriel de E , F est de dimension finie , alors on a
E = somme directe de [ F + (orthogonal de F)]

pour démontrer ça, j'ai :


On considère une base (e1,....,ep) orthonormale de F
On considère l'application f qui à x associe i=1 à p <ei|x>ei.

xE x=f(x) + (x-f(x))

D'où le résultat ???

Merci.

Bon, ok c'est des définitions, mais toute définition a une démo. logique, et internet ne m'en fournit pas (même avec du très haut débit).