Fiche de mathématiques
Ile mathématiques > maths Bac + > Algèbre
 et
et 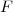 deux ensembles.
deux ensembles.
On dit que est égal à
est égal à 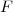 et on note
et on note 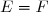 si :
si : 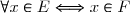
 et
et 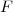 deux ensembles.
deux ensembles.
On dit que est inclus dans
est inclus dans 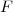 et on note
et on note 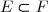 si :
si : 
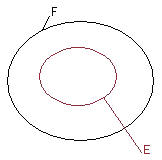
Remarque :
)
 et
et 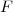 deux ensembles.
deux ensembles.
On appelle intersection de et
et 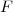 et on note
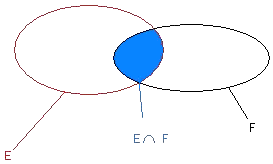
et on note 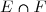 la partie des élements qui sont à la fois dans
la partie des élements qui sont à la fois dans  et dans
et dans 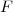 .
.
On a donc
 et
et 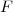 deux ensembles.
deux ensembles.
On appelle réunion de et
et 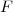 et on note
et on note 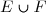 l'ensemble
l'ensemble 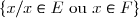
 un ensemble,
un ensemble, 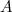 et
et 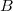 deux parties de
deux parties de  .
.
On appelle différence de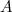 et
et 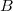 et on note
et on note 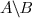 l'ensemble
l'ensemble 

 un ensemble,
un ensemble, 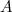 une partie de
une partie de  .
.
On appelle complémentaire de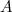 dans
dans  et on note
et on note 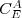 l'ensemble
l'ensemble  /
/ 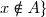
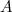 et
et 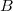 deux ensembles.
deux ensembles.
On appelle différence symétrique et on note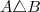 l'ensemble définie par :
l'ensemble définie par :  \cup (B \backslash A))
 un ensemble.
un ensemble.
L'ensemble des parties de est noté
est noté ) et on a :
et on a :  = \lbrace A / A \subset E\rbrace )
On a donc \Longleftrightarrow A \subset E)
Exemple :
Soit
On a alors : = \lbrace \emptyset , \lbrace a\rbrace , \lbrace b\rbrace , \lbrace c\rbrace , \lbrace a,b\rbrace , \lbrace a,c\rbrace , \lbrace c,b\rbrace , \lbrace a,b,c\rbrace \rbrace )
 et
et 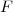 deux ensembles, on définit le produit cartésien qu'on notera
deux ensembles, on définit le produit cartésien qu'on notera 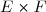 l'ensemble :
l'ensemble :  / a \in E , b \in F \rbrace )
Et on convient : si l'un des ensembles est vide alors :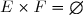
Publié par Panter
le
Ensemble et Application (Partie 1)
I. Théorie des ensembles
a) Egalité
SoientOn dit que
b) Inclusion
SoientOn dit que

Remarque :
c)Intersection
SoientOn appelle intersection de
On a donc

Propriété :
Soient  ,
, 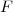 et
et 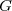 trois ensembles :
trois ensembles :
d) Réunion
SoientOn appelle réunion de
Propriété :
Soient  ,
, 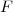 et
et 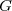 trois ensembles :
trois ensembles :
e) Différence
SoitOn appelle différence de
Propriété :
f) Complémentaire
SoitOn appelle complémentaire de
g) Différence symétrique
SoientOn appelle différence symétrique et on note
Propriétés :
Soient 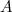 ,
, 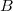 et
et 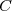 trois ensembles :
trois ensembles :
II. Ensemble des parties d'un ensemble
SoitL'ensemble des parties de
On a donc
Exemple :
Soit
On a alors :
III. Produit Cartésien
SoientEt on convient : si l'un des ensembles est vide alors :
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 algèbre en post-bac
algèbre en post-bac