Inscription / Connexion Nouveau Sujet
Estimation de l'accélération d'un corps
Bonjour.
J'ai un corps qui tourne autour d'un centre C. Le corps est a une distance D du centre C de rotation.
Je souhaiterais avoir une estimation de l'accélération du corps dans son propre repère connaissant sa vitesse de rotation angulaire W.
Quels équations peuvent m'aider pour estimer ça?
Bonjour,
En notation polaire complexe avec origine en et origine des temps appropriée, la position de ton mobile est
(avec
en secondes et
en rad/s. Avec ça tu dois pouvoir te débrouiller ?
Merci pour cette réponse.
En fait je souhaiterai à terme faire le même calcul sur un solid evoluant sur une sphere.
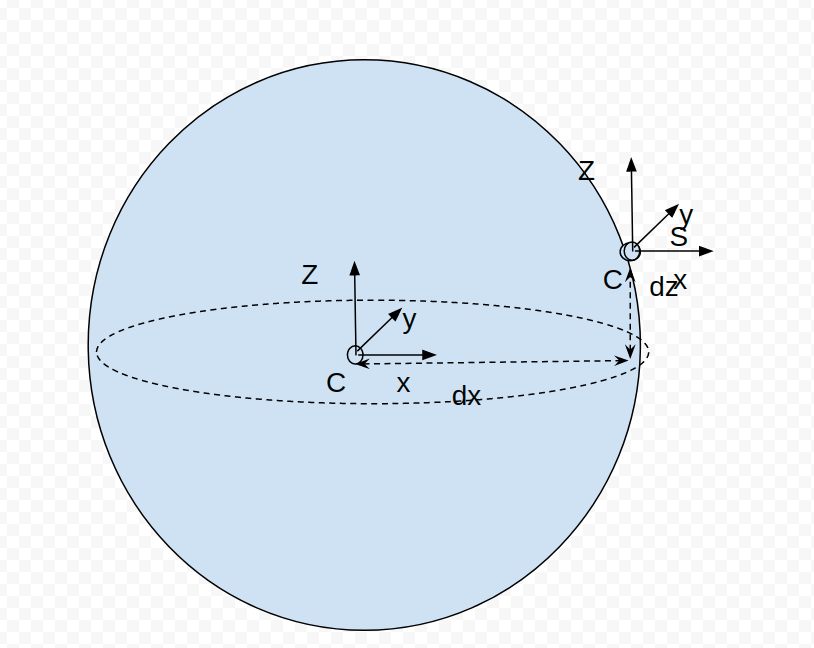
J'ai fait un schéma pour etre plus clair.
J'ai les positions dx, dy,dz de mon mobile par rapport a mon centre. J'ai les vitesses de rotation selon les coordonnées polaire de mon cercle .
Je souhaiterais exprimer l'accélération de mon mobile par rapport au vitesse angulaire wx,wy,wz selon les axes du cercle et les les distances dx,dy,dz dans le repére X/Y/Z du cercle.
Je ne sais pas si c'est applicable également sur ce principe.
Bonsoir,
Ce que tu écris n'est pas très clair :
"coordonnées polaire de mon cercle " ?
"axes du cercle " ?
"repére X/Y/Z du cercle." ?
Tu te places donc dans l'espace à trois dimensions. Si est le vecteur vitesse angulaire (supposé constant ?) pour la rotation d'axe passant par
, la vitesse du mobile
est
.
Pour avoir l'accélération, tu dérives cette formule et la formule du double produit vectoriel te donne , où
est le projeté orthogonal de
sur l'axe de rotation.
En fait je veux modéliser le comportement d'un solide en vrai sur lequel j'ai ajouté une centrale inertielle sur Arduino . La centrale inertielle me donne des infos de vitesse angulaire (wx wy wz) et les accélérations captées (ax,ay, az).
Je voudrais compenser les informations des accélérations sur les axes de ma centrales de mon solide sachant la position angulaire (tangage roulis et lacet) et la vitesses angulaire a chaque Instant. Idéalement si j'arrive à compenser les accélérations, les valeurs devraient être proche de 0.
J'essai de faire un exemple simple en 2D.
Je voudrais exprimer l'accélération sur les axes XZ lors d'une rotation autout de l'axe Y (perpendiculaire à l'écran)
Si dz =0:
az = (wy(k-1) -wy(k) )/dt *dx
ax = 0
par contre si dz est différent de 0 je ne sais pas comment le modéliser, je pensais à ca:
a = tan-1 (dz/dx)
b= 180 -(a +90)
a = norm( dx ,dz ) * (wy(k-1) -wy(k) )/dt
ax = a * cos(b)
az = a *sin(b)
Est ce que mes calculs sont bons?
Y-a-t-il un moyen de faire ca en 3D?


 géométrie en post-bac
géométrie en post-bac