Inscription / Connexion Nouveau Sujet
Etude complète d'une fonction trigonométrique
Bonsoir,
J'ai à nouveau un exercice à faire sur la trigonométrie. J'ai une étude complète de fonction à faire
Voila mon ennoncé et je vais donner mes réponses en même temps:
f
sin(2x- 
/2)
1) Montrer que f est périodique de période
f(x+) = sin(2x+- /2)
= sin (2x- /2)
= f(x)
Donc f est périodique de période
2) Expliquer pourquoi on étudie f dans l'ensemble : [-/2 ;/2]
[-/2 ;/2] est un intervalle de la période
On trace la courbe dans cet intervalle et on déduit le reste de la courbe par des translations de vecteurs
3) Déterminer la dérivée f' de f dans [-/2 ;/2]
f'(x) = cos(2x- /2)
4) Etudier le signe de f' sur [-/2 ;/2]
Je cherche d'abord les valeurs qui annulent :
cos(2x - /2) =cos /2
valeurs qui annulent je trouve 0 et /2
Je ne détaille pas les calculs mais si c'est faux je le ferais !!
Puis je recherche lorsque f'(x)> 0
Et c'est là que je n'y arrive pas parceque je ne sais pas comment faire avec le 2x
Voila ! si vous pouviez défois me corriger et m'aider pour la question 4) afin que je puisse continuer !!
Merci!
Bonsoir,
non, ta dérivée est fausse ...
Rappel : f(x)=sin(ax+b) f'(x) = a*cos(ax+b)
N'oublie pas le a devant !!
bonsoir, 
pour la deuxieme question je crois qu'il faut démontrer que la fonction est impaire ! c'est plus juste
a+
dellys
Ah oui c'est vai j'avais oublié le a devant !
Donc f(x)==2cos (2x - /2)
Non ?
Bon il faut que je refasse la suite !
Je ne vois pas trop ce que c'est les fonctions impaires...
Et merci jamo pour le cadeau ! C'est sympa!
:D
Et pour la question 1, je ne suis pas d'accord non plus !
f(x+PI) = sin[2(x+PI) -PI/2)] = sin(2x+2PI-PI/2) = sin(2x-PI/2+2PI) = sin(2x-PI/2) = f(x)
( car sin(X+2PI) = sin(X) )
Petit rappel sur la parité : 
La parité : fonctions paires et impaires
En fait, ta fonction f est paire ...
Donc, il faut que tu démontres que f(-x)=f(x)
oui jamo (salut
) je pensait que la fonction sin était impaire .. et voila que je vois ton dessin ..
En fait,
Pour la question 4) ça ne change rien parceque divisé 0 par 2 ça reste 0
Donc est ce que les valeurs qui anulent f'(x) sont bien :
x= /5 +k ou x=k ??
Merci !
oui jamo (salut) je pensait que la fonction sin était impaire .. et voila que je vois ton dessin ..
Oui, la fonction g(x)=sin(x) est bien impaire ...
Mais ici, on étudie pas la fonction sinus ...
C'est comme dire que la fonction carrée x² est paire, donc (x+4)² est paire aussi !!
(c'est faux, bien entendu)f'(x)=2cos(2x-PI/2)
f'(x) = 0
<==> cos(2x-PI/2) = 0
<==> 2x-PI/2 = PI/2 +2kPI ou 2x-PI/2 = -PI/2 + 2kPI
Escuse moi,
Je me suis planté en tapant
je voulais dire /2
Mais en fait pour la question de la parité, le prof nous a dit qu'on avait pas encore vu d'exemple mais qu'on le ferais plus tard... donc est ce qu'il n'y a pas un autre moyen pour y arriver sans utiliser la parité ?
je connais pas un autre moyen... (mais la parité moi je l'ai vu en seconde ??)
La parité est pourtant une notion de 2nde ...
Bon, sinon, dans la question 1, on a démontré que la fonction a pour période PI, donc il faut l'étudier sur un intervalle de longueur PI.
Donc [-PI/2 ; PI/2] convient.
De toute façon, si on devait en plus dire que la fonction est paire, on pourrait se contenter d'en étudier que la moitié, c'est à dire que [O;PI/2] puisque le reste se déduit par une symétrie par rapport à l'axe des ordonnées.
D'accord, mais bon en lisant le rappel sur les fonctions paires je me suis mis en tête quelques notions !
Sinon si je marque cela ça suffit pour les premières questions ?
Est ce que vous pourriez m'expliquer un petit peu pour l'inéquation lorsque f'(x)>0 ?
Oui,
f'(x)=0
2cos(2x- /2)=0
2cos(2x- /2)= cos/2
2x-/2 = /2 + 2k
2x = 2/2 + 2k
x = /2 + k
Ou
2x - /2 = -/2 + 2k
2x = 0 + 2k
x = k
Est ce juste pour ces 2 valeurs qui annulent f'(x) ? Ou faut-il faire passer le 2 de l'autre côté des le début ?
Non, c'est bon, le 2 du début, il faut le faire disparaitre tout de suite en fait :
f'(x)=2cos(2x-PI/2)
f'(x) = 0
<==> 2*cos(2x-PI/2) = 0
<==> cos(2x-PI/2) = 0
Maintenant, parmi l'infinité de valeurs que tu viens de trouver (à cause du k), tu dois determiner celles qui sont sur l'intervalle [-PI/2 ; PI/2] ?
ouais
En fait si je comprend bien
La solution ne fonctionne pas puisqu'elle sort de l'intervalle demandé
Par contre /2 est bonne puiqu'il s'agit d'un intervalle fermé et peut donc comprendre cette valeur
Il y aurait donc une seule valeur qui anule f'(x) sur cet intervalle
Non, il y en a plus que ça ...
Tu as 2 familles de solutions :
x = k*PI et x = PI/2 + k*PI
Tu dois essayer toutes les valeurs de k, et garder les valeurs de x si elles conviennent.
Ainsi, pour x = k*PI :
Si k=0 alors x = 0 : OK
Si k=1 alors x = PI : NON
Si k=-1 alors x = -PI : NON
Pour x = PI/2 + k*PI
Si k = 0 alors x = PI/2 : OK
Si k = 1 alors x = 3PI/2 : NON
Si k = -1 alors x = -PI/2 : OK
On a donc en tout 3 valeurs : 0 ; PI/2 et -PI/2.
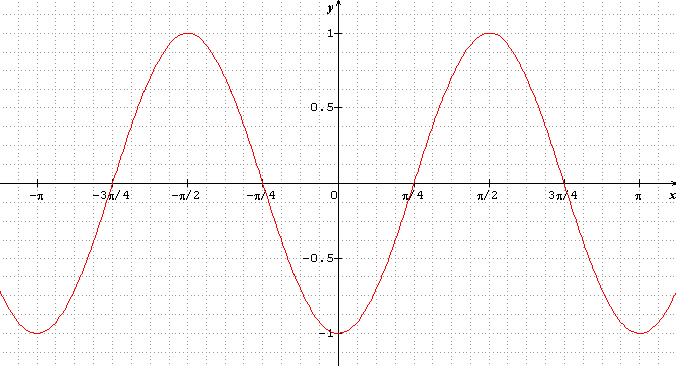
D'ailleurs, tu peux vérifier sur la courbe, c'est bien en 0, PI/2 et -PI/2 qu'on a des extremums, donc là où la dérivée s'annulle ...
C'est vrai j'avais oublié d'essayer avec les différentes valeurs de k !
Par contre pour l'inéquation
f'(x)>0
2cos(2x-/2)>0
cos (2x- /2) >0
est ce que ça veut dire que comme 0 c'est le cosinus de/2, il faut prendre toutes le valeurs supérieur au cosinus de/2
Mais bon je ne pense pas que cela fonctionne puisque il s'agit du cos ( 2x- /2) Et il faut donc tenir compte de ce 2 !
Non, pour l'étude du signe, je te conseile ceci :
tu viens de trouver que f'(x) s'annule en 0, PI/2 et -PI/2
Tu as donc 2 intervalles : [-PI/2 ; 0] et [0 ; PI/2]
Tu n'as qu'à chercher le signe de f'(x) dans chacun de ces 2 intervalles, c'est suffisant ...
Pour cela, prend une valeur dans chaque intervalle (par exemple -PI/4 et PI/4).
Bon, je vais me coucher, bonne continuation, je repasserai demain ...
D'accord
Merci beaucoup pour l'aide et à demain !!
Bonne nuit !
Bon je n'arrive plus à réfléchir
Je regarderais demain au lycée, parceque là je ne comprend pas vraiment tout! J'essayerais de trouver la solution et je reviendrais demain soir pour les explications suivantes si possible !
Et encore merci pour tout le temps passé à m'aider !:D
Bonsoir,
Bon j'ai essayé de voir aujourd'hui pour cette étude de signe, mais je n'ai pas réussit ...
Parceque je ne comprend pas vraiment la façon que tu m'as dites hier soir, car en cours on a l'habitude d'utiliser les inéquations.
Enfin si défois on pouvait m'expliquer ...
Merci !
Ok, reprenons ...
On a trouvé que la dérivée s'annule en -PI/2, en 0 et en PI/2.
Il suffit donc de regarder de quelle signe elle est sur les intervalles [-PI/2;0] et [0;PI/2].
t'es ok avec ce principe ?
oui,
donc en fait dans n'importe quels exemples lorsque on a trouvé les valeurs qui annulent la dérivée, on peut former des intervalles entre ces valeurs ?
Donc, tu prends une valeur dans chaque intervalle.
Dans l'intervalle [-PI/2;0], prenons -PI/4
f'(-PI/4)= 2cos(2*(-PI/4)-PI/2) = 2cos(-PI/2-PI/2)=2cos(-PI)=-2 < 0
Donc la dérivée f' est négative sur [-PI/2;0]
Et en effet, la fonction f est bien décroissante (la courbe descend) ...
D'accord,
Donc il suffit de prendre une valeur dans chaque intervalle et de la remplacer dans la dérivée.
Donc si je m'occupe maintenant de l'intervalle [0;/2] et que je prend /4
f'(/4) = 2cos (2/4 - /2)
= 2cos (0)
= 2
Donc f'(/4)> 0
Donc la fonction est croissante sur l'intervalle [0;/2]
Bon c'est bon j'ai enfin compris !
Et bien pour la fin de l'exercice ça devrait marcher puisqu'il me reste plus que le tableau de variation de f à faire ainsi que la représentation graphique.
En tout cas merci beaucoup pour toute l'aide, c'est vraiment sympa !
Bonne soirée
et à une prochaine fois 
Annuler
connectez vous