Inscription / Connexion Nouveau Sujet
Etude d'une fonction
Bonjour,
La fonction f(x): ln^2(x)+ln(x) définie sur ]0;+infini[ coupe la courbe des abs en deux points A d'abs 1 et B d'abs xb
1)Le minimum de la fonction est -1/4
2)xb strictement plus grand que 1
3)La tangente T à Cf au point B est parallelle à la droite y=e-e^x
J'ai commencé par dérivé f ce qui donne f'(x): 2*(ln x/x)+1/x
J'ai fait f(x)=0 ce qui ma donné x=1 (donc A) et x=1/e (B)
Donc j'ai répondu à la 2) car 1/e est strictement plus petit que 1
j'ai ensuit trouvé la tangente T au pt B grace à :
f'(1/e)=-e
f(1/e)=0
donc la tangente T de Cf au pt B est -ex+1
Donc il faudrait m'aider pour la question 1 et pour savoir si T est parallele à y=e-e^x
bonjour,
bizarre l'énoncé :
La fonction f(x): ln^2(x)+ln(x) définie sur ]0;+infini[ coupe la courbe des abs en deux points A d'abs 1 et B d'abs xb
l'énoncé exacte est :
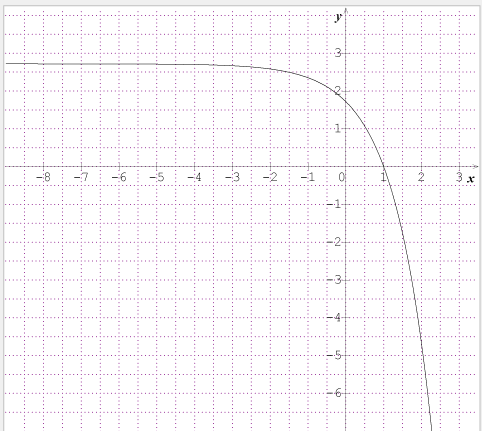
Soit f la fonction définie pout tout x de ]0;+infini[ par f(x) : ln^2(x)+ln(x)
Soit Cf la courbe représentative de la fonction dans un reprére orthogonal OIJ
La courbe Cf coupe l'axe des abscisses en deux points A d'abscisse 1 et B d'abscisee xb
Les 3 questions sont des vrai ou faux
fais le tableau de variation de f
y = e -e^x n'est pas l'équation d'une droite
Oui mais comment le prouver ?
Soit f la fonction définie pout tout x de ]0;+infini[ par f(x) : ln^2(x)+ln(x)
Soit Cf la courbe représentative de la fonction dans un reprére orthogonal OIJ
La courbe Cf coupe l'axe des abscisses en deux points A d'abscisse 1 et B d'abscisee xb
bien. Je ne voulais pas t'ennuyer. Mais c'est différent de l'énoncé de ton tout premier post
kenavo, tu peux aller refaire un tour là ? ![]() DM de mathématiques stp, merci !
DM de mathématiques stp, merci !
Soit f la fonction définie pout tout x de ]0;+infini[ par f(x) : ln^2(x)+ln(x)
Soit Cf la courbe représentative de la fonction dans un reprére orthogonal OIJ
La courbe Cf coupe l'axe des abscisses en deux points A d'abscisse 1 et B d'abscisee xb
Les 3 questions sont des vrai ou faux :
1)Le minimum de la fonction est -1/4
2)xb strictement plus grand que 1
3)La tangente T à Cf au point B est parallelle à la droite y=e-e^x
J'ai commencé par dérivé f ce qui donne f'(x): 2*(ln x/x)+1/x
J'ai fait f(x)=0 ce qui ma donné x=1 (donc A) et x=1/e (B)
Donc j'ai répondu à la 2) car 1/e est strictement plus petit que 1
j'ai ensuit trouvé la tangente T au pt B grace à :
f'(1/e)=-e
f(1/e)=0
donc la tangente T de Cf au pt B est -ex+1
Donc il faudrait m'aider pour la question 1 et pour savoir si T est parallele à y=e-e^x
*** message déplacé ***
malou,
kenavo, tu peux aller refaire un tour là ? [https://www.ilemaths.net/sujet-dm-de-mathematiques-696129.html] stp, merci !
je n'ai pas saisi!
Bonjour
si c'est un vrai faux il faut répondre pour chaque affirmation
1 vrai 2 faux
quant à la troisième il faut revoir le texte n'est certainement pas l'équation d'une droite
--> kenavo : sur le sujet fléché (on y était ensemble tout à l'heure) , on est bien d'accord que la figure est infaisable avec l'énoncé tel que le posteur a écrit ?
Pour la 1 j'ai trouvé il faut faire f'(x)=0 et je trouve e^-1/2 comment faire pour ensuit trouver -1/4 ?
Et non je ne me suis pas trompé mon énoncé dit bien "la droite d'équation y=e-e^x"
le minimum est obtenu pour d'accord
que vaut ?
ou alors vous avez écrit ^ en trop
est bien l'équation d'une droite


 ) :
) :