Inscription / Connexion Nouveau Sujet
Etude d'une néphroïde
Bonsoir à vous,
voici mon problème :
Soit C le cercle de centre 0 de rayon a>0.
Avec les notations de la figure,  est l'enveloppe de la famille des droites Dt passant par A et B.
est l'enveloppe de la famille des droites Dt passant par A et B.
1) Montrer que le point B a pour coordonnées (-acos(3t),-asin(3t)).
2) Déterminer une représentation paramétrique de
 .
.
3) Etudier  et la tracer dans le cas où a=1.
et la tracer dans le cas où a=1.
Je n'arrive pas à montrer que B a ces coordonnées là et quant bien meme je n'arrive pas à sortir une représentation paramétrique. Je dois mal comprendre l'énoncé.
Merci pour votre aide 
Bonjour,
L'énoncé ne le dit pas, mais il y a tout lieu de croire que les angles  et t sont alternes- internes.
et t sont alternes- internes.
Par ailleurs on peut évaluer l'angle entre Ox et OB dans le triangle AOB et en déduire les coordonnées de B.
Bonsoir 
il me semble aussi que c'est à la place de
une idée pour le ,
En considérant le point diamétralement opposé à
on a :
(angle au centre)
et donc (par Chasles pour les angles)
d'où
 sauf erreur de ma part bien entendu
sauf erreur de ma part bien entendu
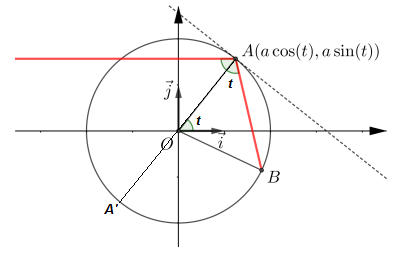
J'aurais dû ajouter " la droite horizontale rouges est sans doute supposée parallèle à l'axe des x" et c'est cela que l'énoncé ne dit pas. De ce fait, t= , les angles étant alternes -internes.
, les angles étant alternes -internes.
Merci à elhor_abdelali de n'avoir pas relevé
Bonjour,
cela correspond à l'une des définitions de la néphroïde :
enveloppe des rayons réfléchis ("caustique") dans un cercle, issus d'une source à l'infini.
Bonjour,
aucune réaction de Mari0, soit c'est trop tard (exo pour avant hier) soit il attend qu'on lui fasse les calculs....
"et quant bien même"
Maintenant qu'on a les coordonnées de B en fonction de t, on peut par calcul déterminer l'enveloppe des droites (AB)
Traditionnellement, et c'est certainement ce qui est attendu dans cet exo, cela se fait en écrivant l'équation de la droite (AB), en fonction de t, Δ(t), et en déterminant la limite du point d'intersection entre Δ(t) et Δ(t+dt) lorsque dt tend vers 0
y' a plus qu'à ...
On peut aussi interpréter cela de façon purement géométrique pour trouver le point de contact de la droite avec son enveloppe.
La détermination de l'enveloppe est alors ramenée à un simple lieu géométrique.
Et on peut prouver alors que la néphroïde ainsi définie est équivalente à une épicycloïde, lieu d'un point d'un cercle (de rayon a/4) roulant sans glisser sur l'extérieur d'un cercle (de rayon a/2)
(cf le site précité qui donne plusieurs définitions équivalentes de la néphroïde, sans les démonstrations)


 géométrie en post-bac
géométrie en post-bac