Inscription / Connexion Nouveau Sujet
Etude de fonction d'un cercle
Bonjour,
cet exercice est surement tout bête mais mon cerveau ne marche pas s.v.p aidez moi je sais pas comment faire expliquer au moins la démarche a faire
Merci D'avance
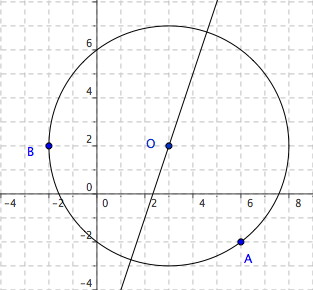
Déterminer une équation d'un cercle dont le centre est situé sur la droite d'équation y=3x-7 et contenant les points A (6 ;-2) et B( -2;2) .
Salut 
Si le centre est sur cette droite et que les points que tu nous donne appartiennent aussi à cette droite alors tu peux nous donner les coordonnées du centre non?

Bonjour
Le cercle va avoir une équation du genre : (x-a)² + (y-b)² = R²
Il faut trouver les coordonnées a et b du centre du cercle et son rayon R , en utilisant les infos données :
le centre est situé sur la droite d'équation y=3x-7 donc b = 3a -7
A est un point du cercle donc (6-a)² + (-2-b)² = R²
B est un point du cercle donc (-2-a)² + (2-b)² = R²
3 inconnues (a , b et R ) 3 équations ! tu devrais pouvoir trouver a , b et R
eh olive_68
Apparament les points A et B n'appartiennent pas à la droite d'équation y = 3x -7
-2  3*6 - 7 et 2
3*6 - 7 et 2  3*2 - 7
3*2 - 7
A oui je n'avais pas vérifié ..
Je ne sais donc surtout pas lire un énoncé..
Merci d'avoir fais la remarque 
re bonsoir ,
je fais une systéme pour les trouvés ?
du genre {(6-a)² + (-2-b)² = R²
(6-a)² + (-2-b)² = R²
dites moi c'est vraiment simple et je doit allé me coucher ou je sais pas 
je comprend vraiment rien c'est pas un devoir noté ni rien mais j'ai vraiment envi d'y arriver et ça m'énerve 
Je t'ai donné le système des 3 équations à résoudre ! ! ! il te faut quoi de plus ? Qu'on le résolve à ta place ! ? !
b = 3a -7
(6-a)² + (-2-b)² = R²
(-2-a)² + (2-b)² = R²
Tu te prends par la main , tu développes , tu réfléchis pour savoir comment annuler certaines inconnues en utilisant la méthode de la combinaison et tu trouves la solution au système !
ok ok ok Merci désoler j'avais mal lu qqch .
Merci a vous est bonne soirée je demande pas qu'on le face a ma place loin de la
j'ai loupé la leçon donc je comprend un peu rien . désoler
merci !