Inscription / Connexion Nouveau Sujet
Etude de fonctions, limites et asymptote
Bjr,
C'est mon premier post : un exo de maths que je n'arrive pas à finir...
1°/ Soit f la fonction définie sur ]-oo ; 0[ U ]0 ; +oo[ par f(x) = sin x
x²
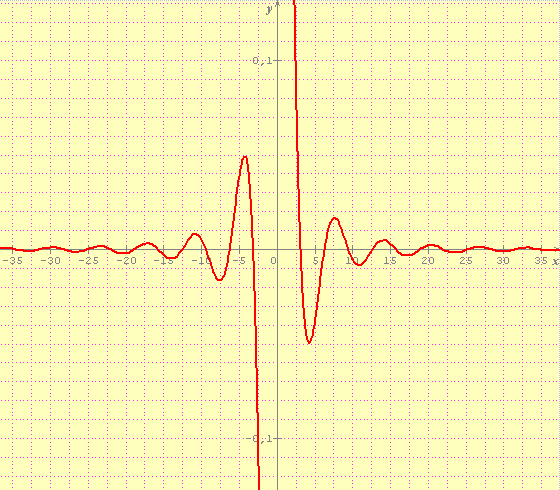
a) Construire la représentation graphique Cf de f sur la calculatrice en prenant d'abord une fenêtre standart puis en prenant x entre -30 et 30, et y entre -0.1 et 0.1 ; la courbe Cf semble-t-elle admettre une asymptote ?
* image externe expirée : merci d'utiliser l'option d'attachement du forum pour éviter ces désagréments *
Oui, x=0
b) Déterminer les solutions de l'équation f(x) = 0 ; quelle est l'interprétation graphique de ces solutions ?
f(x) = 0 sssi le numérateur est nul : sin(x) = 0 <=> x=180(en °) ou
 (en rad)
(en rad)Mais il est écrit les solutions ??? je ne vois qu'une...

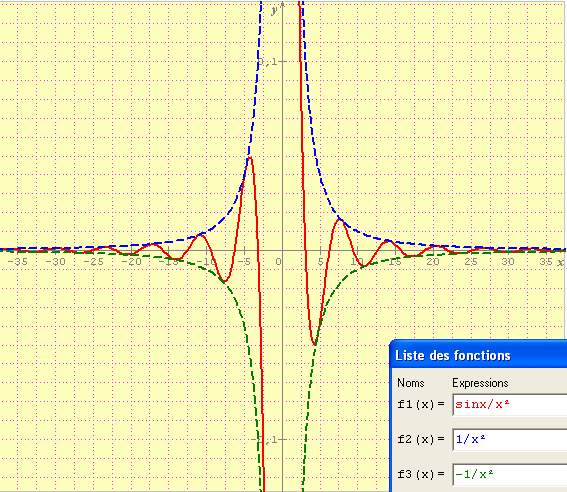
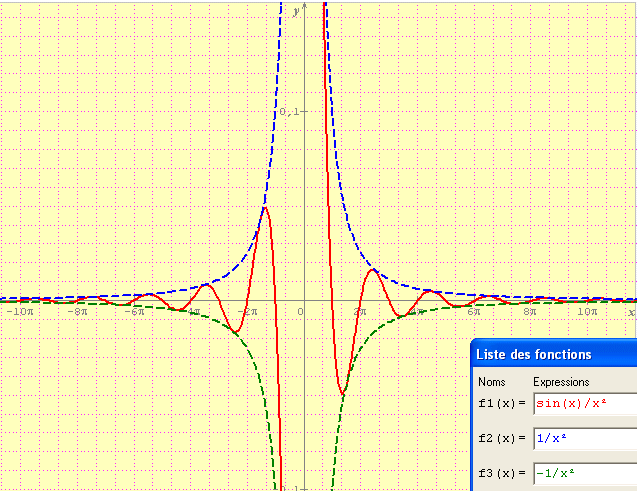
c) Dessiner sur le graphique précédent les courbes représentatives Cg et Ch des fonctions g et h telles que g(x) = 1/x² et h(x) = -1/x²
Quelles conjecture peut-on faire concernant la position de Cf par rapport à Cg et Ch ?
* image externe expirée : merci d'utiliser l'option d'attachement du forum pour éviter ces désagréments *
Là je bloque, peut-être que : x < 1 et x > -1

d) Prouver la conjecture faite à la question c) et déterminer la points d'intersection des courbes Cf et Cg ; déterminter de même les points d'intersection des courbes Cf et Ch.
Merci de m'aider : corriger le débu si il est faut et me guider pour le reste

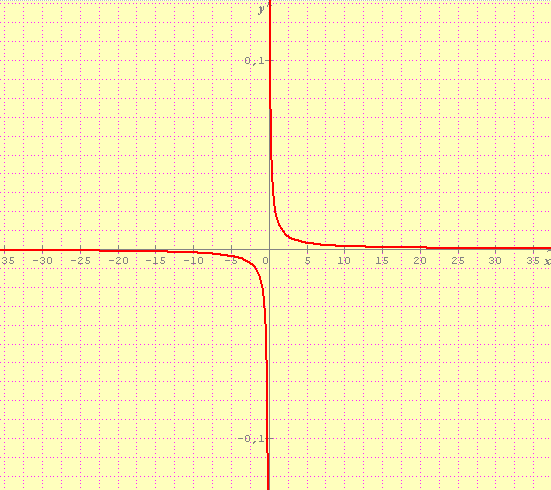
Bonjour et merci mikayaou pour ta rapide réponse, mais je ne comprend pas ta courbe, pourquoi ondule t'elle ? Moi sur ma TI, elle est comme sur "encarta", même en radian.
* image externe expirée : merci d'utiliser l'option d'attachement du forum pour éviter ces désagréments *
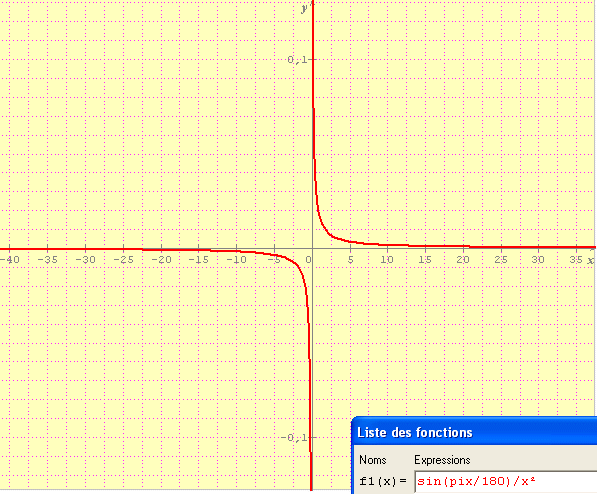
euh, non je suis bien en radian, mais j'avoue être perdu !!! J'ai obtenu une fois avec encarta le même graphique que toi mais je ne sais pas comment...
Magnifique !!! Merci enfin, j'arrive, à tracer une courbe 


Je n'arrivais pas à changer les Xmin Xmax, Ymin, Ymax... Je vais enfin pouvoir revoir mon exo :
Donc l'asymptote est y=0 ?
Les solutions j'en vois toujours qu'une... 
f(x) = 0 si sinx = 0
x=kpi et k non nul
si -30 < kpi < 30
-30/pi < k < 30/pi
-10 < k < 10
18 valeurs d'intersection