Inscription / Connexion Nouveau Sujet
etude de fonctions par derivation
bonjour
etudier par derivation
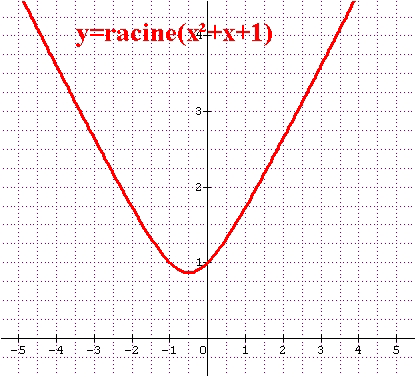
f(x)= (x[sup][/sup]2+x+1)
(x[sup][/sup]2+x+1)

s.v.p j'ai besoin de la méthode pour répondre à des exo similaires

salut
normalement cette fonction est hors programme pour les premiere.
il faut savoir que si u est une fonction derivable en a et v une fonction derivable en u(a) alors
v o u est derivable en a et (v o u)' (a)=u'(a) * v' o u(a)
dans notre exercice :
u(x)=x²+x+1
donc u'(x)=2x+1
v(x)=V(x)=racine carree de x.
v'(x)=1/[2*V(x)]
f(x)=v o u (x)
donc f'(x)=u'(x) * [v' o u(x)]= (2x+1) /[2*V(x²+x+1)]
reste a trouver le signe de f'(x) ...
comment a tu tracer .... (le logitiel)
Bonjour karimovisch,
Tu peux lire la question et la réponse faite ici : ![]() Logiciel de calcul de surface
Logiciel de calcul de surface
Philoux




merci infiniment.....
mais une petite question..."philoux"...puisque je n'habite pas en france...quels sont les ouvrages les plus utiles(shaum ? ...)
Re ,
Je suis inculte en la matière, peut-être que J-P serait à même de te répondre...
Je vous quitte, bonne soirée !
Philoux
ton mail est cependant yahoo.fr ?
Philoux

 Isis
Isis