Inscription / Connexion Nouveau Sujet
Ex fonction exponentielle
Bonjour c'est Robertdu77 ! Je voudrais vous demander de l'aide pour l'exercice suivant :
Jean-Pierre construit un circuit électrique avec un condensateur de capacité C= 0,002 farad qui serait chargé à la base avec une tension E= 10 V, cependant ce dernier se décharge à partir de l'instant t=0 , le circuit contient également une résistance R= 20.000 ohms.
Voici une autre précision : u est la tension du condensateur en fonction du temps t qui s'exprime en seconde.
On justifie la fonction suivante quand t  0 :
0 :
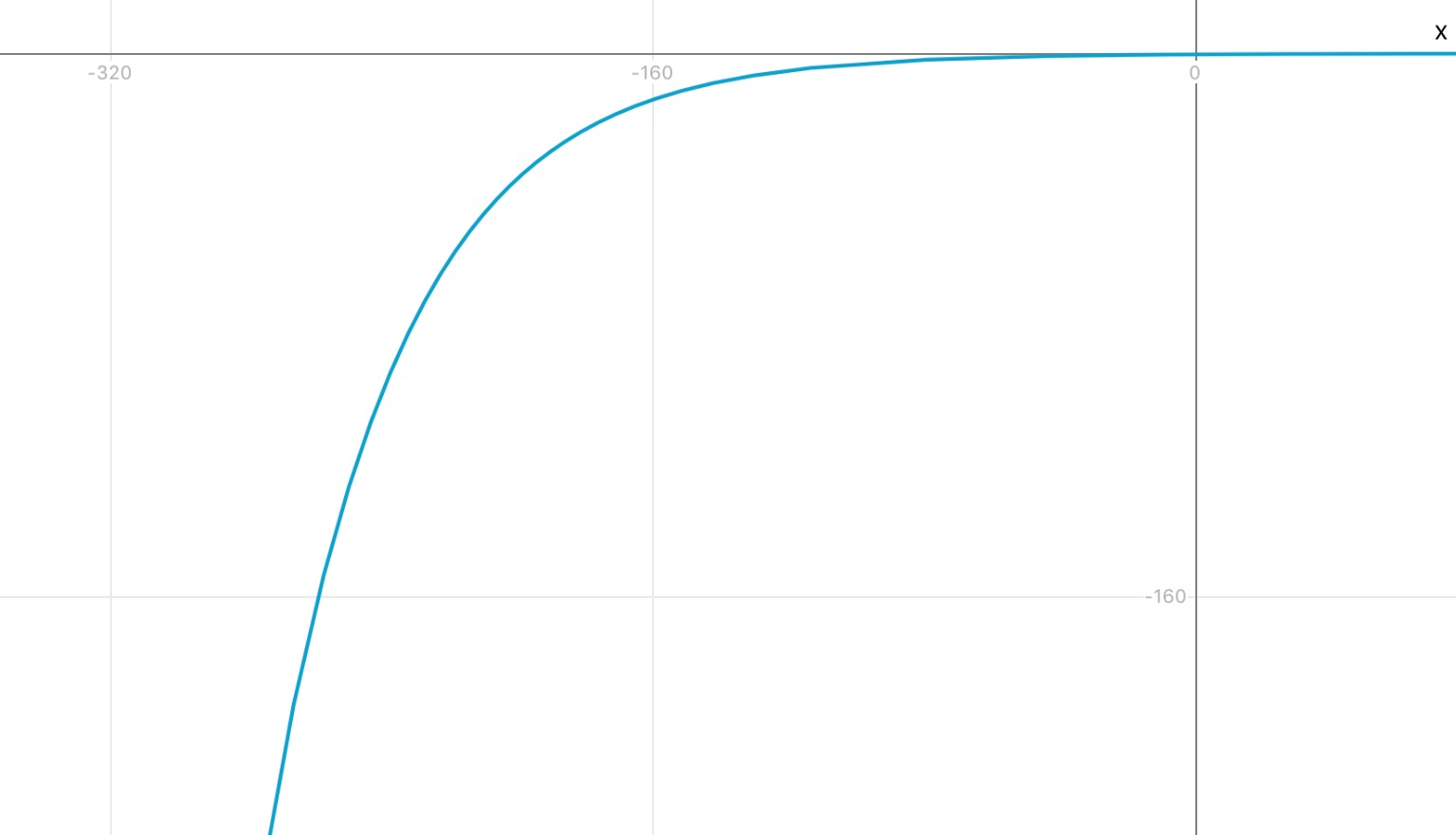
u(t)=E*e-t/RC
Questions:
1) Essayez avec ces informations de donner une expression pour u.
2) Donnez la tension obtenue au bout de 10 secondes.
3) Donner t quand le condensateur est à moitié déchargé
4) Donnez le sens de variations de cette fonction u
5) Interpréter dans la logique de l'exercice.
Mes réponses
1) u(t)= 10*e-t/40
2) 10*e-10/40= 7,788 V
3) t= 28s qui donne 4,9658 V
4) Ici je ne sais pas comment donner le sens de variation, je pense qu'il faut trouver u'(t) mais je ne sais pas comment faire (je ne connais pas la méthode...)
5) Je ne comprends le sens de cette question...
Merci pour votre aide
bonjour
pour les variations, regarde un peu cette fiche ![]() La fonction exponentielle en classe de 1re
La fonction exponentielle en classe de 1re
cela devrait te mettre sur la voie
Bonjour merci pour votre fiche, j'ai essayé tout d'abord de déterminer u'(t) pour la 3):
Je suppose qu'on a ici une forme (uv')x pour u'(t) de u(t)= 10*e-t/40 donc:
-u'(t)=0*e-t/40+ 10*(-1/40)e-t/2
-u'(t)=(-1/4)e-t/2. ( Je suppose donc que la dérivé s'annule en -1/4)
Est-ce correct ?
Merci pour votre aide
un détail...je ne sais pas si en 1re ils voient la dérivée de e^u(x)
si pas, faire ça en composant la décroissance de u avec l'exponentielle
quand j'ai écrit la fiche, j'avais le bO sous les yeux et je n'en parle pas, donc je me pose la question
et pas trop le temps d'aller vérifier là maintenant
Bonjour du coup je trouve
u'(x)=10* (-1/40)*e-t/40
Donc u'(x)= -1/4e-t/40 ?
Mais du coup la fonction s'annule en -1/4 ? (Ça me parait étrange car une fonction exponentielle est toujours au dessus de 0 ?)
Merci
Pourquoi la fonction s'annulerait-elle en -1/4 ?
-1/4 est une constante et l'exponentielle n'est jamais nulle.
Merci mais du coup à quoi sert de trouver le sens de variation de la fonction u dans la 4) vu que cette fonction sera toujours positive ?
Ah oui en effet.. Mais du coup à quoi à quoi consiste la suite de la méthode pour trouver quand u change de variations ?
D'accord merci pour votre réponse , par contre la représentation graphique de u'(t) =-1/4 e -t/40 me bloque. Je ne comprends pas pourquoi u'(t) a des images négatives ?
Merci encore