Annuler
connectez vous
- Cours sur l'aire d'une figure - sixième
- Une carte mentale pour les aires
- Une carte mentale pour les périmètres
- Exercices sur les nombres entiers - sixième
- Bases de géométrie en classe de 6e
- 8 Exercices sur les nombres entiers et décimaux - sixieme
- QCM sur les Angles - Exercice maths 6ème
- Nombres entiers et nombres décimaux - Cours Maths 6ème
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. SixièmeForum de sixième Aire et périmètreTopics traitant de aire et périmètre [tout]Lister tous les topics de mathématiques
Niveau sixième
exercice chevre de Mr seguin
Posté par nadege
Merci j ai besoin d'aide je ne comprend pas.
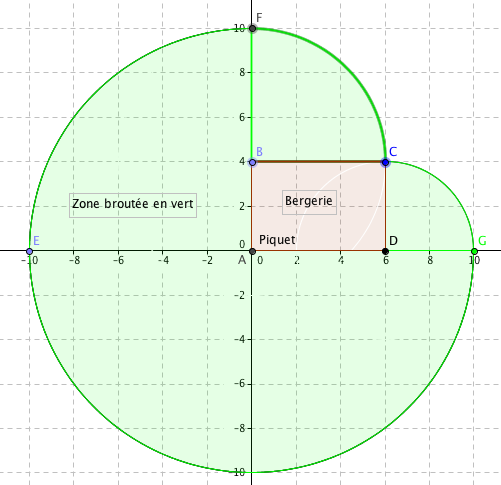
L herbe est haute, il decide de sortir la chevre.Il plante un piquet au coin de sa bergerie qui est une batisse rectangulaire de 6 m de long et 4 m de large, et attache la chevre a se piquet à l aide d 'une corde longue de 10 m . La chevre peut brouter autour de la bergerie toute l'herbe que sa corde lui permet d'atteindre.
1) Realise un dessin (avec les outils de géométrie) qui représente la surface maximale que la chèvre peut ainsi tondre. Tu peut prendre 1 cm sur le dessin pour 2 m dans la realité.
2) Calcule l'aire de cette surface maximale
Bonjour,
Sujet déjà traité ici :
Problème : Chevre de Mr Seguin
Pour repondre a la quetion 2 : J AI FAIT L'AIRE DE LA BERGERIE L*l=6*4=24 m(au carré)
Ensuite j'ai calculé l'aire du cercle pi*r*r=pi*10*10=pi*100=314,16 m(au carré)
Ensuite j'ai fait l'aire du cercle - l'aire de la bergerie = l'aire que la chevre peut brouter soit 290,16 m (au carré)
est ce le bon calcul ,merci de me le dire merci
oui le piquet est placé en A
donc je calcule les 3/' du cercle et ensuite je fais comment pour le reste du quart merci beaucoup
2) Calcule l'aire de cette surface maximale
A max=3/4 de l'aire du cercle de rayon 10 m+1/4 de l'aire du cercle de rayon 6 m+1/4 de l'aire du cercle de
rayon 4 m
Théoriquement si la chèvre est un point :
après la verticale de AB, la corde s'enroule autour du mur en B et peut atteindre le point C (4 m+6 m=10 m) ce qui permet de brouter le 1/4 de cercle de rayon 6 m
après l'horizontale de AD, la corde s'enroule autour du mur en D et peut atteindre le point C (6 m+4 m=10 m) ce qui permet de brouter le 1/4 de cercle de rayon 4 m