Bonjour
1a) tu l'as fait ? qu'est ce qui te gêne ?

J'ai tracé la courbe mais je ne vois pas comment en déduire que f est définie sur R. Cela se voit dans le calcul car il est faisable ...

as-tu toujours le diviser ? 4x²+4x+5 a-t-il le droit de prendre n'importe quelle valeur ?

Je suis désolée mais je ne vois pas ce que vous voulez dire .🤗
Il est juste dit que f est définie sur R donc toutes valeurs possibles...

Non on ne dit pas que f est définie sur R on nous demande de déduire, grâce au graphique, que f est définie sur R.

Tu trouveras l'explication et des exemples pour la 1ère  question ici :

http://www.jybaudot.fr/Analyse/domaine.html

Que peux-dire de ta parabole par rapport à l'axe des abscisses?

L'équation ne doit jamais être nul pour que f soit definie sur R donc vu que la parabole n'a ni d'abscisse ni d'ordonnée nul cela le prouve.
Est ce que ce raisonnement est correct?
Merci

Le raisonnement est bon mais il faut sérieusement revoir le vocabulaire employé...

Le dénominateur de f (donc le polynôme) ne doit jamais s'annuler (ou encore l'équation 4x^2+4x+5=0 ne doit pas avoir de solutions réelles, ou encore, pour tout réels x, l'égalité 4x^2+4x+5=0 ne doit jamais être vérifiée). Etant donné que sa courbe représentative ne croise jamais l'axe des abscisses (du moins, elle en a l'air après lecture graphique), le polynôme ne s'annule jamais.

Voilà, et il faut aussi préciser qu'il n'y a pas d'autres interdictions : le numérateur et le dénimonateur sont trivialement bien définis sur R

question b), à toi de jouer

Pour la question b j'ai calculer la dérivée de la fonction f(x) afin de parvenir au résultat à atteindre.
Mais je ne parviens pas au même résultat, je trouve :
(-8x^2+8x+14)/(4x^2-4x+5)^2

Et bien refais les calculs J'ai pas vérifié l'énoncé. C'est de la forme u/v dont la dérivée est (u'v-uv')/v^2

Ensuite dis moi où f est dérivable.

J'ai refait le calcul trois fois avec cette même formule mais je ne parviens jamais à -2(2x+3)(2x-1)

Ah, et n'oublie pas de factoriser à la fin, en t'appuyant sur l'énoncé. Si tu as du mal à factoriser tu peux développer l'expression de l'énoncé.

salut,
pas d'erreur dans l'enonce.
il faut aller de



à



En route !

Je ne trouve toujours pas après factorisation le bon résultat, je trouve :
8x^2+8x+10-16x^2-8x+8x+4/(4x^2+4x+5)^2
Ensuite
-8x^2+8x+14/(4x^2+4x+5)^2
Pour finir en factorisant
-2(4x^2+4x-7)/(4x^2+4x+5)^2

Je ne trouve pas l'endroit où j'ai fait une erreur ...

Il s'agit d'erreurs de signes, dès la première ligne.

Et ensuite, il faut factoriser le trinôme... Comment on fait ? (pour ça je t'avais dit tu peux développer l'énoncé, c'est plus facile, mais un jour ou l'autre on te donnera pas la réponse !)

Bon, on va pas passer 3h sur comment développer un produit.


Comment on factorise se trinôme ?

J'avais trouvé, je suis en train de factoriser

-2(4x^2+4x+3)
-2(4x^2-2x+6x-3)
-2(2x(2x+3)-1(2x+3))
-2(2x+3)(2x-1)
Désolée pour ma lenteur, je n'avais pas fait de factorisation depuis longtemps 🤗

Oui mais je pense que c'est parce que tu ne connais pas la bonne méthode. Tu as tatonné, petit à petit.

Tu dois avoir un cours sur la factorisation des polynômes. Si le trinôme admet a comme coefficient dominant, et b et c commes racines, alors il s'écrit aussi a(x-a)(x-b).
Il suffisait donc de chercher les racines du trinôme.

On peut chercher des racines évidentes, ou, ici, comme on a déjà la solution, il suffisait de vérifier que 1/2 et -3/2 étaient bien des racines.

Sinon, on peut toujours calculer le discriminant.

Quel est le domaine de dérivabilité, alors ?

pardon, il s'écrit aussi a(x-b)(x-c). Bon on va appeler x1 et x2 les racines plutôt il s'écrit alors a(x-x1)(x-x2)

Le domaine de dérivabilité est R donc )-l'infini ; +l'infini(
?

F est défini sur R donc le domaine de dérivabilité est de -l'infini à+ l'infini

Il faut dire d'où ça sort.
Le dénominateur de f' est celui de f au carré. Celui de f ne s'annule pas, donc celui de f' non plus sur R. Le numérateur et le dénominateur de f' sont biens définis sur R, donc f est dérivable sur R.

Il existe pleins de fonctions non dérivables à des endroits où elles sont définies : par exemple la fonction racine n'est pas dérivable en 0, la fonction valeur absolue non plus.

question c)

Je préfère réctifier : donc f est dérivable dans R partout où elle est définie. Donc dérivable sur R.

C.
Après calcul de f'(x)=0 qui donne deux solutions X1= -3/2 et X2= 1/2
On peut dire que entre - l'infini et -3/2 f'(x) est négative donc f est décroissante. Entre -3/2 et 1/2 f'(x) est positive donc f est croissante . Et entre 1/2 et +l'infini f'(x) est négative donc f est décroissante.

Après la résolution de l'équation, d'inconnue x dans R, f'(x)=0
C'est juste, suivant

Il y a également le minimum trouver suite à la résolution de la fonction f(-3/2) qui est égal à -0.25 et le maximum trouver suite à la résolution de la fonction f(1/2) qui est égal à 0,25.

2a. Sachant que la dérivée de F c'est f(x)Pour cette question j'avais fait y= f(a) (x-a)+F(a) donc y= f(-3/2)(x-(-3/2))+F(-3/2)

Attention il s'agit de minimum et de maximum locaux. J'ai pas vérifié les calculs pour f(-3/2) f(1/2).

Pour la 2), c'est ça. On peut un peu mieux rédiger : "la tangente à la courbe représentative de F en -3/2 a pour équation y=..." ou encore "d : y=..." (dans l'énoncé ils appellent d cette tangente).

Bon l'exercie est terminé, dernière remarque : on ne "résout" pas une fonction. On résout une équation (par exemple f'(x)=0), et on calcule f(-3/2)

Encore une pour le plaisir f(x) c'est un réel. La dérivée d'une fonction n'est pas un réel, mais une fonction. La dérivée de F c'est f, pas f(x).

Ok merci beaucoup pour votre aide 😀🤗
Bonne fin de journée

Une dernière petite question raccroché a cet exercice était b. Des trois courbes ci-dessous, qu'elle est celle qui représente F? Justifiez.
J'ai donc résolu l'équation :
d: y=-0,25×(x-1,5)+0
           -0,25x+0,375
Le problème c'est qu'aucune des courbes ne représentent cette équation.
Je pense donc mettre trompé sur la manière de procéder mais je ne sais pas quoi faire.🤗
Merci

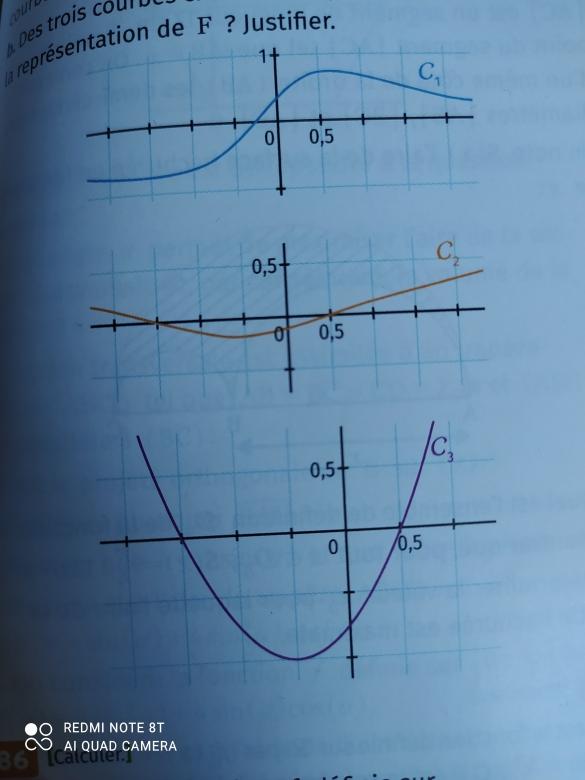
tu n'as pas résolu l'équation... Tu as terminé le calcule de l'équation cartésienne, en faisant encore une erreur de signe.

On sait que F(-3/2)=0
Et que l'équation de la tangente à sa courbe en -3/2 a pour équation : y = ...
Tu peux visualiser la tangente en -3/2, et estimer une valeur facile (par exemple l'ordonnée à l'origine).

Mais il faut déjà corriger ton erreur.

Chacune de ces info te permet d'élminer une courbe.

Evidemment qu'aucune de ces courbes n'est la tangente de F ! Sur le schéma on doit dire laquelle est F !

résoudre une équation c'est chercher l'ensemble des x qui vérifient une égalité. A la fin, on donne l'ensemble des solutions : S = {...}

Bonjour,
J'ai refait mon calcul et trouvé :
-0,25x-0,375.
Pour la suite je ne comprends pas ce qu'il faut faire ...

bonjour
mais d'où sors-tu ce -0,25x-0,375. ??? qui ne veut rien dire d'ailleurs
ta fonction F est définie par F(x)=(2x+1)/(4x^2+4x+5)
c'est celle là que tu dois "retrouver" en éliminant celles qui ne fonctionnent pas (apparemment)

tu as montré que ta dérivée s'annulait en -3/2 et 1/2, en changeant de signes manifestement
il n'y a qu'une seule courbe qui peut répondre à ça à première vue

Donc a première vue c'est la dernière courbe

Mais du coup la dernière courbe c'est la représentation de la dérivée de la fonction F non?...

Enfin, je crois que je me suis mélangée les choses...

Je n'ai rien dit , je viens d'aller voir mon tableau de signe 🤗

alors ?

Alors même en ayant rectifier ce que je venais de dire grâce au tableau de variation, je ne vois pas quel autre calcul ou affirmation faire à part dire que la dérivée s'annule en -3/2 et 1/2...
Faut il chercher la fonction de F par rapport à sa dérivée ?

Ou je réponds en disant qu'ayant calculer l'équation de la tangente au point -3/2, je trouve le coefficient directeur a=-0,25.
Donc la courbe représentative F c'est C2
?