Inscription / Connexion Nouveau Sujet
Exercice de seconde géométrie.
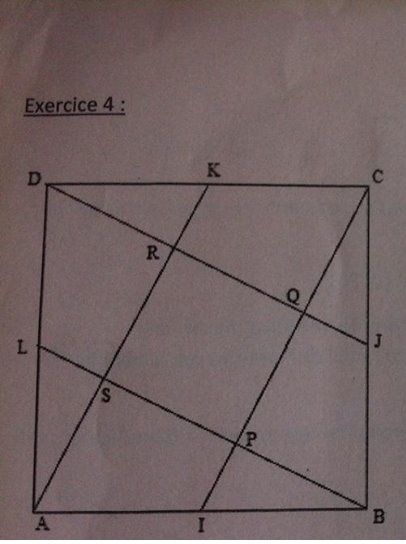
Soit ABCD un carré, I ,J,K et L sont les milieux respectifs de [AB] ; [BC] ; [CD] ; [DA].
S est l'intersection de [Ak]et [BL]
P est l'intersection de [CI] et [BL]
Q est l'intersection de [DJ]et [CI]
R est l'intersection de [AK]et [DJ]
Démonter que PQRS est un carré.
Quelle est le rapport entre son aire et l'aire de ABCD ?
(Figure ci-dessous)
Merci de vos réponses et de votre aide. 
Bonjour,
et quelles sont les pistes que tu as essayées / suivies ? (prérequis dans les règles du forum de dire ce qu'on a essayé et ce qui bloque de façon précise)
- angles (somme des angles d'un triangle, angles complémentaires dans un triangle rectangle, angles avec des parallèles, alternes internes, correspondants etc)
- droite parallèles et parallélogrammes (diverses propriétés des parallélogrammes)
- Thalès ou droite des milieux
- et surtout : symétries de la figure
pour la question de l'aire : il est possible de découper "façon puzzle" cette figure et la réponse devient alors évidente
sinon ... bof, calculs des côtés avec Pythagore etc ...
Bonjour,
J'ai essayé de faire thalès mais je n'ai pas trouvé vraiment de triangle comprenant les bons paramètres. Ensuite j'ai essayé de faire des calculs vectorielles mais non abouti.
Merci de ta première réponse 
Bonjour moi je me suis aidé de vecteurs pour montrer que RQPS est un parallelograme. Mais je ne sais pas comment démontrer que ce parallelograme est un carré. Merci de votre aide 
Thales ou droite des milieux permet de justifier que PS = PB etc si besoin (par exemple pour calculer le côté de PQRS, ou simplement pour justifier que les cotés de PQRS sont égaux (parallélogramme et angles droits ne suffisant pas pour en faire un carré)
considérer les angles (angles complémentaires et angles égaux) pour montrer que le triangle ASB est rectangle en S car ses angles en A et en B sont complémentaires (angle LBA = angle KAD par symétrie, ou en invoquant lourdement les tangentes de ces angles)
Paudua : il y a plus simple que les vecteurs
KC et AI parallèles et égaux (chacun à la moitié du côté de ABCD), donc KCIA est un parallélogramme etc ...
tout cet exo est en fait totalement élémentaire et la seule difficulté est la rédaction correcte.
en tout cas il y a de très nombreuses façons de le faire.
un peu chacun la sienne.
démonstration expéditive en une ligne :
l'ensemble de la figure est globalement inchangé par rotation de 90° autour du centre du carré ABCD etc


