Inscription / Connexion Nouveau Sujet
Exercice dérivabilité de Fonction
Bonsoir, je doit faire un exercice pour demain en maths, mais je suis bloqué... Si vous avez des pistes à me donner je suis preneur  Merci beaucoup.
Merci beaucoup.
L'exercice:
Soit la fonction définie par f(x)=  (x2+2x) et soit sa courbe représentative dans le plan rapporté à un repère (0;i, 1)
(x2+2x) et soit sa courbe représentative dans le plan rapporté à un repère (0;i, 1)
1) Déterminer l'ensemble de définition de f et étudier sa continuité.
2) a)Déterminer les limites de f aux bornes de son ensemble de définition
b) Démontrer que la droite  d'équation y= x+1 est asymptote oblique à Cf au voisinage de +
d'équation y= x+1 est asymptote oblique à Cf au voisinage de + .
.
c) Démontrer que la droite A' d'équation y-x-1 est asymptote oblique à au voisinage de - .
.
3) a)Etudier la dérivabilité de f, en particulier en 0 et en -2
b) Déterminer la fonction dérivée de f, étudier le sens de variations de f et dresser son tableau de variations
4) Montrer que la droite d'équation x -1 est axe de symétrie de Cf
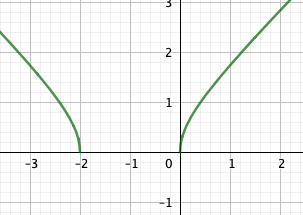
5) Tracer dans le repère (0; ;
; )
)
Ce que j'ai déjà fait:
1) f(x)=  (x2+2x)
(x2+2x)
Df =  /(x2+2x
/(x2+2x 0)
0)
Df = ]- ;-2]
;-2] [0;+
[0;+ [
[
Sur ]- ;-2] et [0;+
;-2] et [0;+ [, f coïncide avec des fonctions polynômes, donc f est continue sur chacun des intervalles.
[, f coïncide avec des fonctions polynômes, donc f est continue sur chacun des intervalles.
2) a) Lim (x +
+ )= +
)= +
Lim (x -
- ) = -
) = - 
b) Je fais f(x) - (x+1) et trouve une limites en + qui vaut 0, j'en déduit donc que la droite est bien asyptote oblique au voisinage de +
qui vaut 0, j'en déduit donc que la droite est bien asyptote oblique au voisinage de + 
Voilà ensuite je suis bloqué...
Merci de votre aide
Merci, j'ai essayé pour -2, mais je trouve une forme indéterminé:  (x2+2x)/x+2, et donc c'est indéterminé lorsque je cherche la limite en -2...
(x2+2x)/x+2, et donc c'est indéterminé lorsque je cherche la limite en -2...
Oui mais je trouve  h2-2h/h
h2-2h/h
Donc quand h tend vers 0 on a 0/0, ce qui est une forme indéterminé, donc je ne comprend pas..
Donc en -2, ça tend vers 0 et en 0 ça tend vers + . Es-ce bien celà ? Merci de votre aide. J'ai fait la question b), il ne me manque que la 4 ensuite....
. Es-ce bien celà ? Merci de votre aide. J'ai fait la question b), il ne me manque que la 4 ensuite....