Inscription / Connexion Nouveau Sujet
exercice difficile sur les dérivé
Bonjour, j'ai un devoir a rendre et j'avoue que je ne comprends aboslument par l'exercice j'aurais donc besoin de votre aide
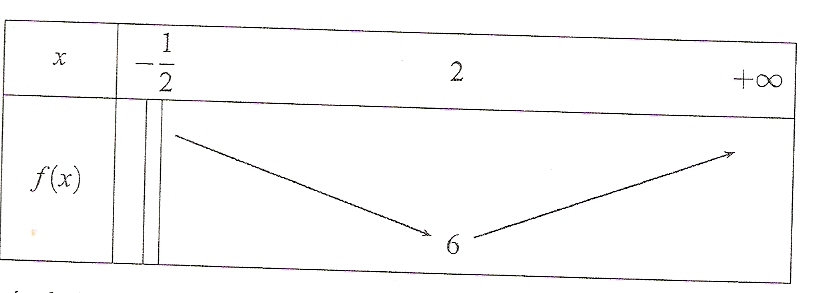
Soit f une fonction définie et dérivable sur l'intervalle ]-1/2 ; +[ dont le tableau de variation est ci-dessous.
1. On note f' la dérivée de la fonction f. Déterminer f'(2)
2. Déterminer les réels a et b tels que f(x) = ax+b+25/2x+1. (On connait f(2) et f'(2))
3. On admet que f est la fonction définie sur l'intervalle ]-1/2 ; +[ par f(x)=2x-3+25/2x+1.
Justifier par le calcul les résultats obtenus dans le tableau de variation.
https://www.ilemaths.net/img/forum_img/0546/forum_546357_1.jpg
( adresse du tableau )
Merci par avance
bonjour, merci de la réponse rapide !
premièrement je n'ai pas réussi a le mettre désolée!
ensuite voila ce que j'ai trouvé sans grande certitude :
1) f(x) = ax=b
f'(x) = a
f'(2) = 2
2) f(x) = ax+b+ 25 / 2x+1
j'ai essayé d'utiliser la dérivée U'V- V'U / U2 ( au carré )
mais je n'arrive pas a la dérivée correctement et a trouver une équation a deux inconnus
3) f(2) = 6
alors f(2) =(2*2) -3 + ( 25/2*2 +1) = 6
résultat du tableau vérifié
c'est d'ailleurs pour cela que je demande de l'aide, ca va bientot faire 2 jours que je penche sur ce sujet donc voila
du coup la fonction f est croissante, sur I mais je ne comprends pas bien a qu'elle question cela va m'aider?
si vous l'aviez écrit correctement j'aurais dit oui mais 2 =0!!!!!!
les parenthèses sont indispensables
d'où première équation en
et
calculez en fonction de
et
ensuite écrivez que seconde équation en
et
puis résolvez le système vous devriez avoir et
f'(2)= a + 25 [ -2 / ( 4+1) 2 ( au carré )] = 0
= a ( -2/25) = 25
f'(2)= a = 0,5
je trouve ca bizzare, encore faux non?
il vous reste à vérifier le tableau de variation donc de vérifier le signe de
soit si vous ne l'avez fait
de rien