Bonjour,

conjecturer = deviner en observant sur la calculette l'existence ou pas d'un minimum et la/les valeur(s) de x qui rend(ent) f_λ(x) minimale

pour la b il faut faire bien plus que ces hypothèses car il faut distinguer tous les cas
selon que x-1 est >0 ou <0
que x-2 est >0 ou <0
et que x-4 est >0 ou <0

donc pas seulement deux cas à traiter

pour la b) tu peux t'organiser avec un tableau
regarde sur cette fiche un exemple traité ainsi Un exercice classique comportant des valeurs absolues

Pour la a) ducoup avec la calculatrice ça donnerai ;
minimum de f2 atteint pour x=2
minimum de f3 atteint pour x=2
minimum de f4 atteint pour x=4

je vais essayer la b) avec la fiche

L'indication de l'énoncé  "pour x>=0" a-t-elle une importance ?

oui, bien sûr, cela réduira ton ensemble d'étude et donc ton tableau dans lequel x variera seulement entre 0 et +

ca me donne :

x-1>=0 équivaut à x>=1
sur [0;+1[ : |x-1| = -x+1
sur [1;+inf[ : |x-1| = x-1

x-2>=0 équivaut à x>=2
sur [0;2[ : |x-2| = -x+2   ---> 2|x-2| = -2x+4
sur[2;+inf[ : |x-2| = x-2 ---> 2|x-2| = 2x-4

Pour le dernier terme je ne sais pas car λ est variable ?
Merci

oui, mais c'est un simple coefficient au même titre que le 2 devant la valeur absolue précédente
tu fais de même pour ta valeur absolue et ensuite tu multiplies tout simplement ton résultat par

x-4>=0 équivaut à x>=4
sur [0;4[  : |x-4| = -x+4 ---> λ|x-4| = -λx+λ4
sur [4;+inf[  : |x-4| = x-4 ---> λ|x-4| = λx-λ4

Donc (si cela est juste) maintenant, je fais un tableau avec x allant de 0 à +inf (avec les valeurs 1, 2 et 4)
et pour chaque ligne je mets un des trois termes et leur écriture selon l'intervalle du tableau. En dernière ligne je fais la somme des trois écritures de la colonne entre chaque intervalle (comme sur votre fiche) .
Le problème est que je ne vois pas le rapport avec la question a), car il faut démontrer les résultats cités plus haut...

oui, c'est ça la méthode
on verra pour le lien avec la question a) ensuite

Alors pour l'intervalle [0;1] j'ai trouvé -λx+λ4-3x+5  (je ne sais pas si on peut faire qqchose avec ce λ ?)
[1;2] : -λx+λ4-x+3
[2;4] : -λx+λ4+3x-5
[4;+inf] : λx-λ4+3x-5
Ainsi que des valeurs nulles pour |x-1| avec x=1 et 2|x-2| avec x=2, et avec lambda (3ème ligne) je me suis dit qu'on ne pouvait pas savoir...
Est-ce bon ?
merci

il te manque ton intervalle [0 ; 1 ]
sinon, c'est parfait

Je l'ai mis dans ma réponse précédente, pour l'intervalle [0;1] ça me donne -λx+λ4-3x+5 !
Et ducoup je ne comprend pas le rapport avec la a)... Faut-il remplacer λ par 2,3 puis 4 ?

je n'avais pas vu car il était en tête
tout est OK
alors
mets chacune de ces formes sous la forme Ax+B
......
à chaque fois cela est une fonction affine
une fonction affine admet-elle un extremum ?
......donc quelles possibilités ? ......

pour la première par exemple cela donnerai
-𝛌x+𝛌4 - 3x+5
----->    -𝛌x-3x+𝛌4+5 ? ou y'a-t-il d'autres modifications à faire ?

salut

une remarque :

f(x) = |x - 1| + 2|x + 2| + a|x - 4| pour x >= 0 et a >= 0 (d'après l'énoncé)

donc on en déduit que f(x) >= 0 et que f admet un minimum pour tout réel a

carpediem, oui, d'accord
question on ne peut plus mal formulée sans doute
peut-être veut-on lui faire dire que sur un certain intervalle et pour une valeur bien particulière de , ce minimum n'est pas unique....

salut,
je pense que le but est de preciser les valeurs de x pour lesquelles f est minimale

Que dois-je faire maintenant ?

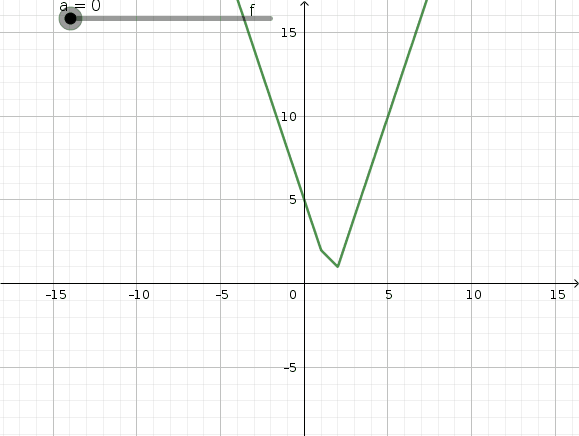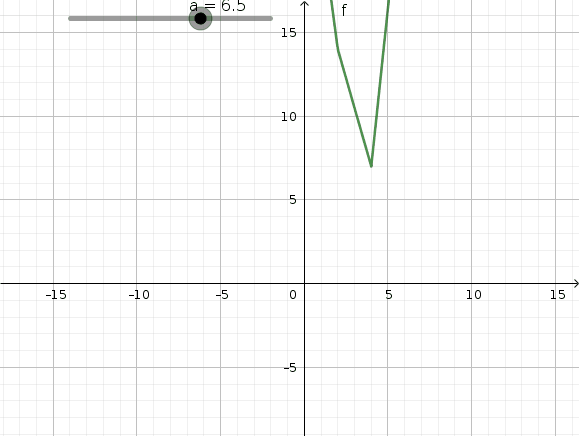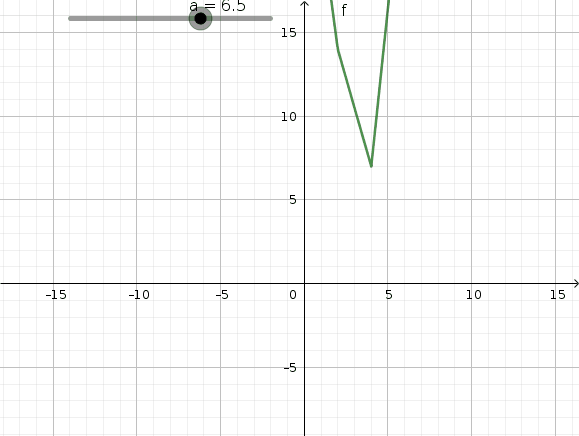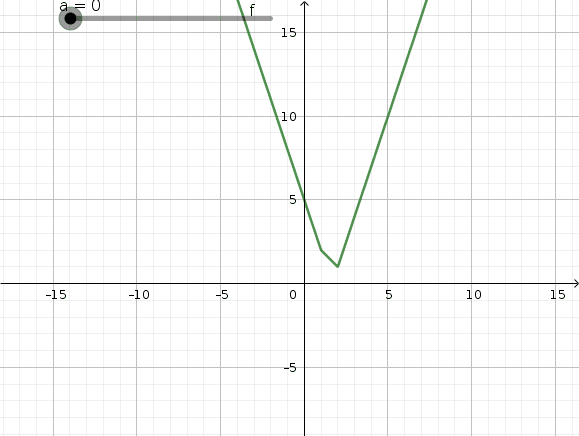
On peut voir que pour lambda=3, f(x) admet un minimum pour toute les valeurs de x comprises dans l'intervalle [2;4]

3 cas à etudier lambda<3, lambda=3 et ...

et bien 𝛌>3 ? Mais cela est pour la question a) ou b) ?

b/

Désolé mais je ne comprend plus...
j'ai fait un tableau avec des valeurs absolues selon l'intervalle de x,  j'ai essayé de mettre mes résultats sous la forme ax+b et je ne sais pas s'ils sont justes, et je ne vois pas le rapport avec 𝛌 >ou=ou< a 3 ??

fais un tableau des variations pour lambda<3. Conclus

quand 𝛌<3, f𝛌 (x) est décroissante en ]-inf; 2[ minimum en 2 puis est croissante en ]2; +inf[
Mais qu'en conclure ? Et à quoi sert mon tableau pour les valeur absolues

oui mais tu l'as demontre ?

et bien on m'a demandé de conjecturer donc non...

la question a/ est terminee
maintenant on demontre !

Voici mon tableau de simplification de la fonction (c'est tout ce que j'ai pu faire) :
1ère colonne : -x+1 + 2(-x+2) + 𝛌(-x+4)
2ème colonne : x-1 + 2(-x+2) + 𝛌(-x+4)
3ème colonne : x-1 + 2(x-2) + ?𝛌-x+4)
4ème colonne : x-1 + 2(x-2) + 𝛌(x-4)
Donc on a f𝛌 (x) simplifiée comme demandé dans la question b), mais en quoi cela démontre les résultats de la a) ??

que de temps perdu !

c'est-à-dire ?

Mettre chacune des formes trouvées sous la forme Ax+B , avec A et B deux réels.

f λ ( x ) = − x + 1 + 2( − x + 2 ) + λ( − x + 4 ) = − x + 1 − 2 x + 4 − λ x + 4 λ = − 3 x − λ x + 5 + 4 λ Puis x en facteur : ) −( 3 + λ )x + 5 + 4 λ qui est une fonction affine décroissante puisque λ > 0 et donc −( 3 + λ ) < 0

Pour moi, il faut calculer f2, f3, f4 dans chaque intervalle du tableau mais je trouve la question 1 bizarre, parce que simplifier f λ ( x ) c'est procéder justement avec le tableau...

en principe on pourrait se contenter de calculer les images de 0, 1, 2, 4
puis en deduire les variations
puisque la fonction est monotone sur chacun des intervalles

Donc par exemple pour lambda=2
on remplace lambda par 2 dans −x ( 3 + λ )  + 5 + 4 λ :
− x( 3 + 2 )  + 5 + 8 = -3x-2x+13 = -5x+13
puis a<0 la fonction est décroissante
puis après on change d'écriture.....
et on déduit le minimum de la où la fonction commence à croître ?

calcule les images en fonction de lambda

j'utilise la formule simplifiée ou celle de l'énoncé ?

celle de l'enonce

pour λ=2 :
x=0 ça donne 13
x=1 ça donne 8
x=2 ça donne 5
et x=4 ça donne  7

pour λ=3
x=0 ça donne 17
x=1 ça donne 11
x=2 ça donne 7
et x=4 ça donne  7

pour 𝛌=4
x=0 ça donne 21
x=1 ça donne 14
x=2 ça donne 9
et x=4 ça donne 7

lambda=a dans la suite
f(x)=|x-1| + 2|x-2| + a*|x-4|
f(0)=1+4+4a=4a+5
f(1)=??
etc

f0 = 4a+5
f1 = 3a +2
f2 = 2a+1
f4 = 7

Moi , pour faire une démonstration rigoureuse, je ferais 3 tableaux de variations avec la forme simplifiée sous la forme d'une fonctions affine par morceaux :
un dans le cas où < 3
un dans le cas où = 3
un dans le cas où > 3

Mais je peux me tromper.

on peut mais on risque d'y passer le reveillon
il faudra y revenir

sinon
4a+5>3a+2>2a+1 donc f est decroissante sur [0;2]
ensuite voir si 2a+1 peut etre egal à 7 puis inf à 7 puis sup à 7

c'est ce que j'ai fait, mais est-ce que cela permet de démontrer les résultats de la quesiton a) ? c-a-d :
min de f2 atteint pour x=2
min de f3 atteint pour les valeurs de x E (2;4)
min de f4 atteint pour x=4

Pour le tableau enfait j'ai mis les équation simplifiés avec les valeurs x et lambda .
si je fais un tableau pour lambda=2, j'obtiens alors 4 équations affines qui constituent la fonction et j'obtiens une fonction strictement décroissante sur [0;2] puis stricement croissante sur [2;+inf[, donc on en déduit que le miniimum est 2 ce qui correspond avec les résultats citée ci-dessus

Pareil pour le tableau de lambda = 3
cela me donne une fonction décroissante sur [0;2]
puis une constante (parallèle aux abscisses) en [2;4]
puis une fonction affine croissante en [4; +inf[

Résultat cohérent aussi pour lambda=4...

Ces résultats correspondent avec le graphe animé de Malou
ainsi, pour moi, on a bien répondu à la question en simplifiant flambda (x) et en démontrant clairement avec des tableaux de variations...

Mais peut-être que moi aussi je me trompe, (bien que pour moi cela est juste)

c'est bien mais une demo generale oblige à prendre lambda quelconque
cad ne pas donner de valeur à lambda

sous réserve d'une erreur de recopie toujours possible.....

je pense qu'en récapitulant les calculs ainsi, il est facile de démontrer qu'on a toujours un minimum et pour quelle(s valeur(s) de x

comme a > 0
on est sûr des variations pour 3 intervalles sur 4

le minimum peut donc être soit en x=2, soit en x=4, soit on a un plateau pour a=3

et il est facile de savoir si c'est x=2 ou x=4 suivant a, puisque f(2)=1+2a et que f(4)=7