Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première DérivationTopics traitant de dérivation [tout]Lister tous les topics de mathématiques

1 2 +

Niveau première
Partager :

Exercice Fonction dérivée et points

Posté par
Ugo272 08-04-21 à 10:29

Bonjour, j'aimerai une réponse à mon problème :

On considère la fonction f définie sur C par f(x) = 2- \frac{2(1-x)}{(x^{2}+1)}


On note Cf sa courbe représentative.
1) a- Justifier que f est dérivable sur C et montrer que pour tout réel x, f′(x) = \frac{-2(x^{2}-2x-1)}{(x^{2}+1)^{2}}


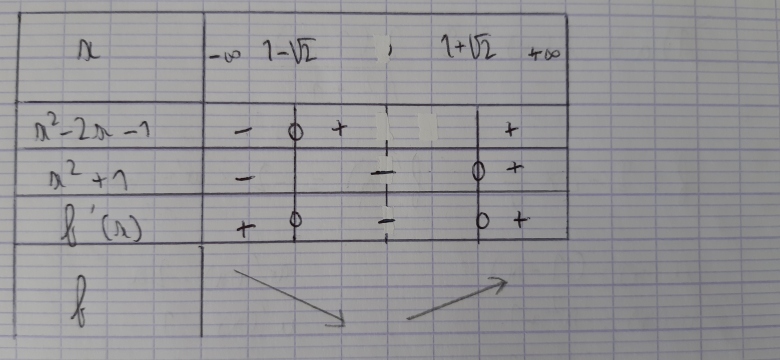
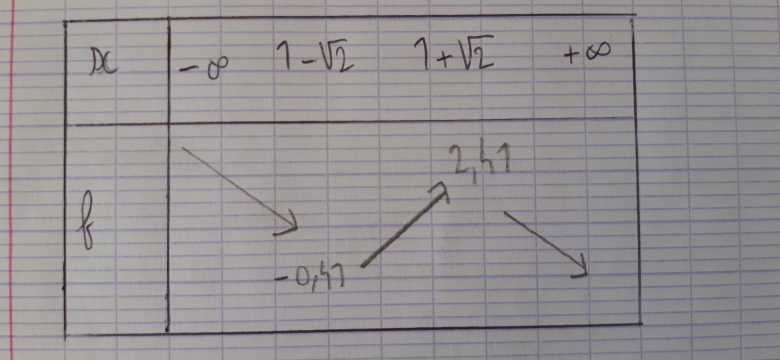
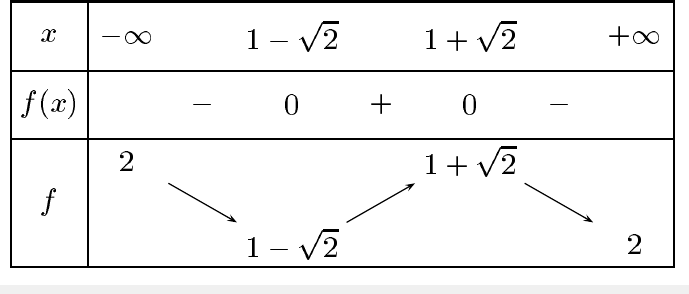
b- Etudier le signe de f′(x) puis dresser le tableau de variations de f.
On calculera les valeurs exactes des extremums.

2) Déterminer l'équation de la tangente (T) à Cf au point A d'abscisse 1.

3) On veut montrer qu'il existe un point B de Cf tel que la tangente à Cf en B soit parallèle à la droite D d'équation y = −x.

a- Montrer que le problème revient à résoudre l'équation x4+4x+3 = 0.

b- Vérifier que  x^{4}+4x+3 = (x+1)^{2}(x^{2}-2x+3)

c- Conclure.

4) Déterminer les coordonnées du point d'intersection entre Cf et la droite D ' d'équation y = 2.
Etudier la position relative de la courbe représentative Cf avec la droite D '.

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 10:33

Bonjour

Que proposez-vous ?  Qu'avez-vous effectué ?

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 10:39

Bonjour,
hé bien pour la dérivée je ne sais pas si c'est u/v ou le numérateur c'est k*u est donc = à k*u' et ensuite cela devient 1/v ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 10:44

Vous auriez pu essayer

f= 2-2\times \dfrac{u}{v}\quad f'(x)=-2\times \dfrac{u'v-v'u}{v^2}

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 10:46

Mais 2-2=0. Pourquoi ce serait -2 ?

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 10:55

J'ai donc fais \frac{1(x^{2}+1)-2x(1-x)}{(x^{2}+1)^{2}}
ensuite x^{2}+1-2x+2x^{2}
et on obtient (2x^{2}-2x-1) ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 10:56

La dérivée d'une fonction constante  est 0 et (kg)'=kg'

f'=0+k\left(\dfrac{u}{v}\right)'

C'est ce que j'avais écrit

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 10:58

https://latex.ilemaths.net/ile_TEX.cgi?(x^{2}-2x-1)%20? c'est plutot ca

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 10:58

x2-2x-1

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:01

Il manque la multiplication par -2 et (1-x)'=-1 et non 1

et 2+1 =3 alors que 2-1=1

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:07

\frac{1(x^{2}+1)-2x(1-x)}{(x^{2}+1)^{2}}
x^{2}+1-2x+2x^{2}
et on obtient (x2-2x-1)/(x2+1)2
en rajoutant le -2, on a -2(x2-2x-1)/(x2+1)2

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:13

Ensuite l'étude du signe on peut pas faire delta ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:16

Il ne faut pas oublier les balises
vous avez écrit

\dfrac{{\textcolor{red}{-1}}(x^{2}+1)-2x(1-x)}{(x^{2}+1)^{2}}

{\textcolor{red}{-1}}x^{2}{\textcolor{red}{-1}}-2x+2x^{2}

d'où x^2-2x-1

reste à multiplier par -2  et remettre le dénominateur   f'(x)=\dfrac{-2(x^2-2x-1)}{(x^2+1)^2} \\

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:19

On peut  calculer \Delta, mais aussi remarquer que

-1=1-2   et donc x^2-2x-1=(x-1)^2-2

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:20

D'accord. J'écris {\textcolor{red}{-1}}x^{2}{\textcolor{red}{-1}}-2x+2x^{2} dans le détail de la dérivée ?

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:21

Donc je fais le delta de x2-2x-1 ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:21

(1-x)'=-1  Il faut donc bien écrire la dérivée comme il faut

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:38

Je fais le delta de x2-2x-1
Cela donne : b2-4*a*c
= (-2)2-4*1*(-1)
=8
8>0 donc deux racines

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:38

Je n'obtient pas des valeurs exacte pour les racines

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:42

Non, quelle importance ?

x_1=1-\sqrt{2}\quad x_2=1+\sqrt{2}

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:45

D'accord oui obtient ça

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:50

Signe de f'(x), variation  et tableau

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:51

Pouvez vous me dresser le tableau de variations car je ne sais pas comment vous l'envoyer.

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 11:52

et pour calculer les extemums,  on remplace les x de la fonction f(x) initiale par les valeurs x1 et x2?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 11:57

Comme une image, mais seulement le tableau  voir FAQ question 05

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:01

Je fais le tableau de signe sur mon brouillon et je vous l'envoie en photo ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 12:07

mais que le tableau

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:20

Vous pouvez vérifier que f(1-\sqrt{2})= \frac{6-2\sqrt{2}}{3}
et f(1+\sqrt{2})= \frac{8-3\sqrt{2}}{2}

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 12:26

f(1-\sqrt{2})=1-\sqrt{2}

f(1+\sqrt{2})=1+\sqrt{2}

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:28

tableau

Exercice Fonction dérivée et points

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:29

je n'ai pas compris votre réponse. Pourquoi les valeurs des extremums seraient identiques avec les racines ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 12:38

Que faites-vous du -2 ? ou comment un trinôme du second degré ne s'annule qu'une fois en changeant de signes

Comment la somme de deux nombres positifs peut-elle être négative  ?

Comment peut-on avoir une valeur qui annule le dénominateur  alors que l'ensemble de définition est \R ?

3 intervalles  2 flèches ?

Pour le nouveau tableau  n'oubliez pas de faire aperçu avant  il y a grande chance que vous renvoyez le même
Il faudra faire Ctrl +F5 avant.  Le texte sera supprimé, mais l'image conservée

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:45

Après le delta pour l'étude du signe, j'ai dis que le dénominateur est strictement positif et que donc f'(x) >0, est-ce juste ?
Ensuite j'ai fais un tableau de signe alors que c'est pas demandé donc je vais l'enlever
Donc je dois faire 3 flèches ?
Quelles sont les valeurs des extremums ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 12:51

Ce sont les calculs

f(1-\sqrt{2})=2-\dfrac{2(1-(1-\sqrt{2}))}{(1-\sqrt{2})^2+1}=2-\dfrac{2\sqrt{2}}{4-2\sqrt{2}}=2-\dfrac{\sqrt{2}}{2-\sqrt{2}}=2-\dfrac{\sqrt{2}(2+\sqrt{2})}{(2-\sqrt{2})(2+\sqrt{2})}

f(1-\sqrt{2})=2-\dfrac{2\sqrt{2}+2}{2}=2-(1+\sqrt{2})=1-\sqrt{2}

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:51

Tableau

Exercice Fonction dérivée et points

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 12:54

Mais ce n'est pas ce que vous avez écrit

Il n'y a pas besoin de tableau  n'intervient que le signe d'un trinôme et son produit par -2
Il y a bien 3 intervalles

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 12:58

Si il y a un tableau, cela est demandé dans la consigne.
Je fais celui que je vous ai envoyé avec 3 flèches et les valeurs des extremums ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 13:04

Il est demandé un tableau de variation, mais pas de tableau de signes

Le dernier envoi est quasiment vide

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:04

Tableau

Exercice Fonction dérivée et points

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:06

je mets plutôt les valeurs exacts pas d'approchées?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 13:12

Le texte dit  : valeur exacte
Oui  le tableau est correct
Exercice Fonction dérivée et points

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:16

Très bien merci. Mais pourquoi vous avez mis 2 aux infinis ?

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:17

Pourrions nous continuer à 14h ?

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:18

Et l'équation de tangente est bien y : f = f'(1)(x-1)+f(1) ?

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 13:25

C'est vrai qu'en première vous n'avez pas encore vu les limites
Quand x va tendre vers l'infini f(x) va tendre vers 2

l'équation de la tangente en 1 est y=f'(1)(x-1)+f(1)

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 13:27

D'accord

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 13:30

À tantôt

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 14:26

Rebonjour.
Alors pour l'équation de tangente je trouve pour f(1)=2 et f'(&)=-1 ou 1.

Posté par
heklare : Exercice Fonction dérivée et points 08-04-21 à 14:31

y=1(x-1)+2x=x+1

Il n'y a pas le choix  l'image par une fonction est unique

Posté par
Ugo272re : Exercice Fonction dérivée et points 08-04-21 à 14:40

D'accord donc le résultat est y= 1(x-1)+2x = x+1?

1 2 +


Rechercher
Menu
Espace membre
47 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !