Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

exercice fonction Ln

Posté par
billydu13 02-03-11 à 14:34

Bonjour , j'ai un exercice a faire pour la rentrée et je ne sais pas comment m'y prendre pour determiner une limite et enlever la forme indeterminée , quelqu'un aurait il la gentillesse a me l'expliquer ? Je vous en remercie d'avance

voici l'exo :

determiner les limites aux bornes :

a) f(x)=x2 +3x-xln(x)
j'ai dit que la fonction est definie sur +* car ln est definie sur +*

Etudions la limite de f en + :

f(x)=x(x+3-lnx)=x(x+3+ln(1/x)) et la je crois que c'est encore une forme indeterminée donc je ne sais pas quoi faire

et aussi faut il demontrer que lim ln(1/x) qd x+= -


sinon la suite de l'exercice c'est :

b) f(x)=(x)lnx +1

c) f(x) = xln(1+1/x) sur +*

et d) f(x)=(lnx)/(x-1) sur ]1;+[

je vous remercie beaucoup de votre aide
cdlt bill

Posté par
dhaltere : exercice fonction Ln 02-03-11 à 14:44

f(x)=x(x+3-lnx)=x(x+3+ln(1/x))
tu peux expliquer ?

Posté par
billydu13re : exercice fonction Ln 02-03-11 à 19:24

salut dhalte , en fait j'ai pu deduire cela car -ln(x)=ln(1\x)

on sait que ln(a\b)=ln(a)-ln(b)

ici , ln(1\x)=ln(1)-ln(x)=ln(e0)-ln(x)=-ln(x)

voila sinon tu n'as aucune idée pour calculer la limite dans la question a ?

merci d'avance
cdlt bill

Posté par
dhaltere : exercice fonction Ln 02-03-11 à 19:35

oui, effectivement

ça m'avait paru incongru parce que la solution est tellement plus simple

f(x)=x^2 +3x-x\ln(x)

Comportement en +\infty

Que connais-tu du cours ? \lim_{x\rightarrow+\infty}\frac{\ln(x)}x=0

essayons alors de faire apparaitre cette forme

f(x)=x^2 +3x-x^2\frac{\ln(x)}x

c'est bien sûr toujours indéterminé, mais pas pour longtemps :

f(x)=x^2(1 +\frac3x-\frac{\ln(x)}x)

Ce qui est dans la parenthèse tend vers 1
ce n'est plus une forme indéterminée.

Voilà

Posté par
billydu13re : exercice fonction Ln 03-03-11 à 15:06

okay je te remercie javais oublié que pour calculer une limite le plus simple est de factoriser par le plus "haut" terme , en l'occurence ici x2

du coup ca fait que lim f(x) x+=+

pour ce qui est de la limite en - voila ce que j'ai fait :

soit f(x) = x2(1+3/x-lnx/x)

lim x2 x-=+

lim 3/x x-=0

lim lnx/x x-=0

DONC(produit) lim f(x) x-=+

est ce juste ? merci d'avance
cdlt bill

Posté par
dhaltere : exercice fonction Ln 03-03-11 à 19:18

la limite en -\infty ?

tu as dit toi-même que f(x) était définie sur \mathbb{R}^{+*}=]0;+\infty[

Pour une raison très simple, et je pensais que tu l'avais bien en tête : le logarithme népérien \ln(x) n'est défini que pour x>0

Posté par
billydu13re : exercice fonction Ln 03-03-11 à 19:40

arrhhh mince !! je suis tombé dans le panneau

Donc en fait les limites aux bornes qu'il faut calculer dans les cas a) b) c) d)  sont seulement en + et en 0+

cdlt bill

Posté par
dhaltere : exercice fonction Ln 03-03-11 à 19:41

eh oui.

Posté par
billydu13re : exercice fonction Ln 04-03-11 à 11:11

je suis désolé mais il y a encore une chose sur laquelle je bloque , c'est pour calculer les limites aux bornes de la fonction :

limite en +

f(x) = x*ln(1+1/x)

je sais que lim x x+=+
            lim 1/x x+=0
            lim ln(1+1/x) x+=0
            

j'aurais donc tendance à dire que lim f(x) x+=0 mais cela ne correspond pas graphiquement

quant à la limite en 0+ ; lim f(x) x0+=0

et derniere chose , pour la d): f(x) = (lnx)/(x-1)
peut on dire :lim lnx/x x+=0
donc lim (lnx)/(x-1) x+=0 ??



merci de ton aide
cdlt bill

Posté par
dhaltere : exercice fonction Ln 04-03-11 à 13:54

f(x)=x\ln(1+\frac1x)

comportement en +\infty

l'argument du logarithme tend vers 1, donc le logarithme tend vers 0. Multiplié par l'inconnue x qui tend vers +\infty, nous avons ici une forme indéterminée 0\times\infty !

Citation :
j'aurais donc tendance à dire que
ben non

Pur résoudre cette forme indéterminée, il faut procéder en deux étapes.

Premier résultat : montrons quelque chose qui va te paraitre d'abord assez éloigné du problème actuel :
montrons que \lim_{h\rightarrow0}\,\frac{\ln(1+h)}h=1

Pour cela, considérons l'expression T(h)=\frac{\ln(1+h)}h

nous avons aussi T(h)=\frac{\ln(1+h)-\ln(1+0)}{h-0}

Quelle bizarrerie, non ? Pourquoi faire ça ?
Parce que ce rapport est le taux de variation de la fonction g(x)=\ln(1+x) entre le point d'abscisse 0 et le point d'abscisse 0+h. Or la limite de ce taux de variation lorsque h tend vers 0 est le nombre dérivé en 0 de la fonction g.

Or g est dérivable en tout point (sauf -1, mais il ne nous intéresse pas ici), et sa fonction dérivée vaut : g'(x)=\frac1{1+x}

Donc g'(0)=1

et comme nous avons vu que \lim_{h\rightarrow0}\,T=g'(0), nous avons finalement le résultat annoncé.

C'est un résultat et une méthode à retenir

posons maintenant x=\frac1h

et dans ce cas :
\frac{\ln(1+h)}h=x\ln(1+\frac1x)

Quand h tend vers 0 (par valeurs positives), x tend vers +\infty

d'où le résultat :
\lim_{h\rightarrow0\\h>0}\,\frac{\ln(1+h)}h=\lim_{x\rightarrow+\infty}\,x\ln(1+\frac1x)=1

De la même manière
\lim_{h\rightarrow0\\h<0}\,\frac{\ln(1+h)}h=\lim_{x\rightarrow-\infty}\,x\ln(1+\frac1x)=1

Et quand x tend vers 0 ?
D'abord ce ne peut être que par valeurs positives. Dans le cas contraire, le logarithme n'est pas défini.

Ensuite : x\ln(1+\frac1x)=x\ln(\frac{x+1}x)=x\(\ln(x+1)-\ln(x)\)=x\ln(1+x)-x\ln(x)
Le premier terme, x\ln(1+x) est le produit de x qui tend vers 0 par le logarithme dont l'argument tend vers 1, donc qui tend vers 0 aussi : ce n'est pas une forme indéterminée : x\ln(1+x) tend vers 0.

Le second terme x\ln(x) demande plus d'attention :
il est le produit de x qui tend vers 0, par \ln(x) qui tend vers -\infty, d'où une forme indéterminée.

Un résultat de classe que tu dois connaitre nous rappelle que \lim_{x\rightarrow0\\x>0}\,x\ln(x)=-1

Mais je te le redémontre, parce que il fait intervenir un autre résultat de cours encore plus important à retenir :

Posons alors h=\frac1x

Alors x\ln(x)=\frac{\ln(\frac1h)}h=\frac{-\ln(h)}h

Et LE résultat que tu dois absolument retenir (on vous l'a surement démontré, mais la démonstration est plus théorique et a moins d'importance jusqu'au BAC)

\lim_{h\rightarrow+\infty}\,\frac{\ln(h)}h=0

Donc en résumé :
\lim_{x\rightarrow0\\x>0}\,x\ln(x)=\lim_{h\rightarrow+\infty}\frac{\ln(h)}h=0

Et nous pouvons alors conclure, puisque dans la somme x\ln(1+\frac1x)=x\ln(1+x)-x\ln(x), les deux termes tendent vers 0 :
\lim_{x\rightarrow0}\,x\ln(1+\frac1x)=0

exercice fonction Ln

tu as encore à montrer la limite en -1, non ? Elle est plus facile, celle-là

Posté par
billydu13re : exercice fonction Ln 04-03-11 à 14:36

re , waouu je te remercie infiniment dhalte CA c'est de la demonstration !!

quant à la limite en -1 je croyais que lorsqu'une fonction integre ln ( definie sur +*), il ne fallait calculer que la limite en + et en 0+ ??

cdlt bill

Posté par
dhaltere : exercice fonction Ln 04-03-11 à 20:07

Citation :
lorsqu'une fonction intègre ln
Qu'est-ce que entends par là ?

Veux-tu dire "lorsqu'une fonction utilise ln" ?


Dans ce cas : attention

g(x)=\ln(x) est effectivement définie uniquement pour x\in]0;+\infty[

mais h(x)=\ln(1+\frac1x) est définie pour
x\neq0 car il faut pouvoir calculer \frac1x

et surtout
1+\frac1x>0 car l'argument du logarithme doit être strictement positif.
C'est pas x qui doit être >0, c'est l'argument du logarithme.

Maintenant, il reste à résoudre l'inéquation 1+\frac1x>0 pour savoir quelles sont les valeurs de x autorisées pour la fonction h(x)=\ln(1+\frac1x).

La réponse est ]-\infty;-1[\cup]0;+\infty[

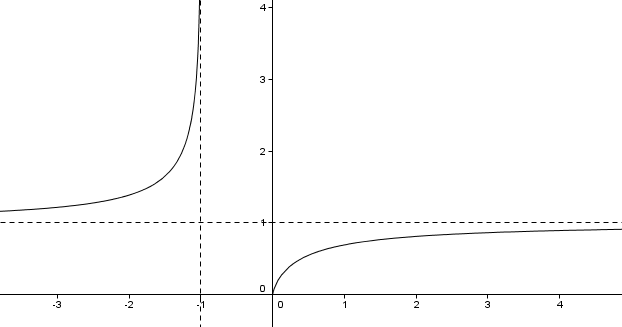
Et le graphe de cette fonction a deux branches, l'une sur le premier intervalle, l'autre sur le second.
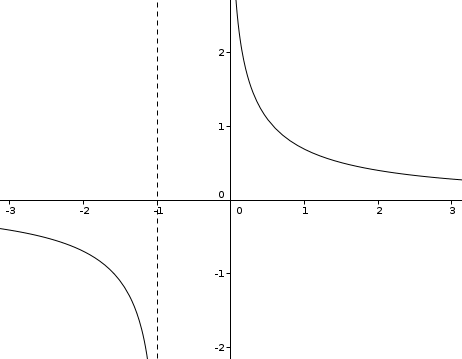
exercice fonction Ln

c'est pareil par exemple avec la racine carrée

\sqr x n'est définie que pour x\ge0

mais la fonction
g(x)=\sqr{x+3} est définie pour x+3\ge0, c'est à dire x\ge-3


Rechercher
Menu
Espace membre
12 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !