Inscription / Connexion Nouveau Sujet
Exercice fonctions & variations
Bonjour, et bonne nouvelle année !
Voici l'énoncé d'un exercice :
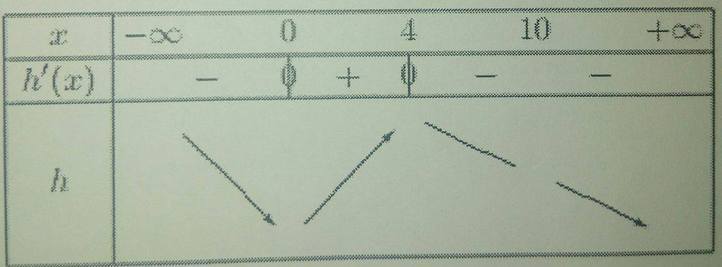
"Soit h la fonction définie sur  par h(x) = -x3+6x2+1. Le tableau de variation de h est le suivant [photo jointe n°1]
par h(x) = -x3+6x2+1. Le tableau de variation de h est le suivant [photo jointe n°1]
a) Recopier et compléter le tableau de variations.
b) Montrer que l'équation h(x)=0 n'admet pas de solution sur l'intervalle ]- ;4]
;4]
c) Montrer que l'équation h(x)=0 admet une unique solution sur l'intervalle ]4;10]
d) A l'aide de la calculatrice, donner un encadrement d'amplitude 10-2 de cette solution
e) Calculer la dérivée seconde de h(x)
f) Compléter le tableau de façon à faire apparaitre la convexité de h ainsi que toutes les informations que l'on peut déduire de cette analyse."
Et voici ce que j'ai commencé à faire :
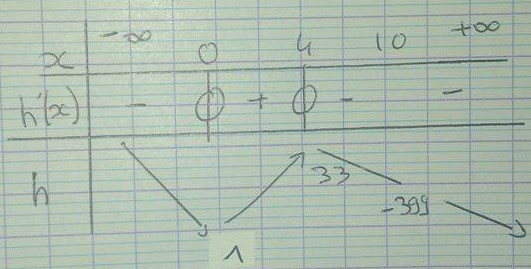
a) Mon tableau [photo jointe n°2]
Ensuite je ne me rappelle plus comment faire pour trouver les solutions. J'aurai pu utiliser delta mais ce n'est pas sous la bonne forme. Du coup je bloque :/
Merci d'avance pour votre aide ! 
Bonjour,
Tu dois compléter ton tableau avec les limites quand x tend vers - et +  .
.
Ensuite, applique ton cours (th. des valeurs intermédiaires)
Pour x entre 0 et 4, f(x) prend toutes les valeurs de [1;33], pas de 0 là-dedans ....
D'accord donc je dois dire
b) D'après le théorème des valeurs intermédiaires l'équation h(x)=0 n'admet pas de solution sur l'intervalle ]- ;4] car elle n'est ni monotone ni continue
;4] car elle n'est ni monotone ni continue
c)D'après le théorème des valeurs intermédiaires l'équation h(x)=0 admet une unique solution sur [4;10] car elle est monotone et continue sur cet intervalle.
Par contre quelle est cette solution ? Car avec la calculatrice quand j'entre h(x) dans le menu et que je regarde la table ça ne me donne pas une seule et unique solution. Après je ne sais pas vraiment si c'est là qu'il faut chercher :/
ouhlala tu mélanges...
pour appliquer le TVI, il faut obligatoirement;
que la fonction soit monotone sur l'intervalle considéré
que la fonction soit continue sur l'intervalle considéré
et que la valeur k étudié (ici 0) appartienne à [f(a);f(b)] avec a et b des réels
D'accord donc je dois dire
b) D'après le théorème des valeurs intermédiaires l'équation h(x)=0 n'admet pas de solution sur l'intervalle ]-
 ;4] car elle n'est ni monotone ni continue
;4] car elle n'est ni monotone ni continue
non, entre -
 et 0, pas de solution puisque valeurs entre +
et 0, pas de solution puisque valeurs entre + et 1(donc pas de passage à 0); de même entre 0 et 4....Il faut distinguer chacun des intervallles où la fonction est monotone. Remarque : il n'y a pas de discontinuité, je me demande où tu en vois !
et 1(donc pas de passage à 0); de même entre 0 et 4....Il faut distinguer chacun des intervallles où la fonction est monotone. Remarque : il n'y a pas de discontinuité, je me demande où tu en vois !
c)D'après le théorème des valeurs intermédiaires l'équation h(x)=0 admet une unique solution sur [4;10] car elle est monotone et continue sur cet intervalle où elle varie de +33 à -399, donc passe par 0
Par contre quelle est cette solution ? Car avec la calculatrice quand j'entre h(x) dans le menu et que je regarde la table ça ne me donne pas une seule et unique solution. Après je ne sais pas vraiment si c'est là qu'il faut chercher :/
Avec ta calculatrice, tu devrais trouver h(6.02)=+0.2 et h(6.03)=-0.09
donc solution entre ces 2 valeurs.
Une idée pour la c → h est continue et strictement décroissante sur ]4;10]. 0 est compris entre 4 et 10. Donc d'après le théorème des valeurs intermédiaires l'équation h(x)=0 admet une unique solution dans ]4;10]
Avec ta calculatrice, tu devrais trouver h(6.02)=+0.2 et h(6.03)=-0.09
donc solution entre ces 2 valeurs.
Ah oui c'est pour la d) d'accord j'ai compris
Oups ça ne devait se trouver là ça ^^
Ce n'est pas 0 qui est entre 4 et 10...
Entre 4 et 10 pour la variable, la fonction varie de +33 à -399 en prenant (TVI) une fois chacune des valeurs intermédiaires, elle passe donc 1 fois par 0
h est continue et strictement décroissante sur ]4;10]. 0 est compris entre 4 et 10. Donc d'après le théorème des valeurs intermédiaires l'équation h(x)=0 admet une unique solution entre f(4)=33 et f(10)=-399 ?
Quand x varie entre 4 et 10, h(x) varie entre 33 et -399.
On est dans un intervalle où h est continue et monotone , donc, d'après le TVI, h(x) passe 1 fois et une seule par 0 (parce que -399<0<33).
Imagine le graphe : on coupe 1 fois l'axe des abscisses.
D'accord, je crois que j'ai compris ça. Je visualise mieux la situation.
Du coup ma dernière proposition pour la c) est juste ou non ?
Et pour la b) je ne sais pas trop quoi mettre parce que déjà h n'est pas strictement monotone sur ]- ;4]
;4]
h est continue et strictement décroissante sur ]4;10]. 0 est compris entre 4 et 10. Donc d'après le théorème des valeurs intermédiaires l'équation h(x)=0 admet une unique solution entre f(4)=33 et f(10)=-399 ?
je ne peux pas te laisser écrire que 0 est entre 4 et 10 !
Je t'ai proposé :
Quand x varie entre 4 et 10, h(x) varie entre 33 et -399.
On est dans un intervalle où h est continue et monotone , donc, d'après le TVI, h(x) passe 1 fois et une seule par 0 (parce que -399<0<33).
tu as la réponse depuis 18h28...
D'accord donc je dois dire
b) D'après le théorème des valeurs intermédiaires l'équation h(x)=0 n'admet pas de solution sur l'intervalle ]-
 ;4] car elle n'est ni monotone ni continue
;4] car elle n'est ni monotone ni continue
non, entre -
 et 0, pas de solution puisque valeurs entre +
et 0, pas de solution puisque valeurs entre + et 1(donc pas de passage à 0); de même entre 0 et 4....Il faut distinguer chacun des intervallles où la fonction est monotone. Remarque : il n'y a pas de discontinuité, je me demande où tu en vois !
et 1(donc pas de passage à 0); de même entre 0 et 4....Il faut distinguer chacun des intervallles où la fonction est monotone. Remarque : il n'y a pas de discontinuité, je me demande où tu en vois !




