Inscription / Connexion Nouveau Sujet
Exercice géométrie
Bonjour, j'ai un exercice de géométrie à faire mais je suis un peu perdue et bloquée.
Pourriez-vous m'aider ?
Voici l'énoncé :
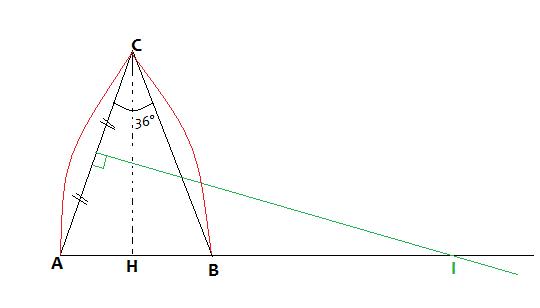
ABC est un triangle isocèle tel que AC = 10cm et ACB = 36°. La médiatrice de [AC] est (AB) en I. On trace le cercle de centre I passant par A et C. L'arc AC est un arc d'ogive. On trace le symétrique de cet arc dans la symétrie d'axe (AC).
Les deux arcs forment une voûte d'ogive. Le but le l'exercice est de calculer la longueur de cet voûte d'ogive.
1) Démontrez que le triangle CIB est isocèle.
2) a. Démontrez que AI = 10(1+2cos72)
b. Déduisez-en que la voûte d'ogive a pour longueur :
4 (1+2cos72)
(1+2cos72)
c. Donnez de cette longueur une valeur approchée à 1 cm près.
Je vais joindre le schéma de la figure.
Voici ce que j'ai fait :
1) ( je ne suis pas tout du sûre de mon raissonnement mais j'ai fait ceci):
Comme le triangle ABC est isocèle alors AC = CB = 10cm.
Comme la médiatrice de [AC] coupe (AB) en I alors AI = CA
donc le triangle ACI est isocèle, comme B  [AI] alors le triangle CBI est isocèle.
[AI] alors le triangle CBI est isocèle.
2) ici je ne sais pas quoi faire donc j'ai essayé de décomposer :
AI = 10(1+2cos72)
AI = BI + AB
(ensuite j'ai essayé de calculer certains côtés avec la trigonométrie mais cela ne m'a pas été utile, car ça ne consernait pas les côtés qui m'étaient utiles).
3) ici je n'ai rien trouvé
4) la voûte d'ogive mesure environ 20 cm
Merci d'avance pour votre aide

1) Je n'ai pas bien compris ta démonstration.
Je raisonnerais plutôt sur les angles, en calculant la valeur des angles CAB et BCA, puis CIB et BCI afin de montrer que ces deux derniers sont égaux.
Merci de ton aide.
Cependant, en utilisant ce que tu me dis ; j'arrive à calculer les angles CAB et CBA, lesquels mesurent chacun 72°,mais ensuite je n'arrive pas à calculer CIB et BCI, j'ai quand même résonné de cette façon :
comme ABI est un angle plat alors CBI = 180 - ABC
CBI = 180 - 72
CBI = 108°
De là, je ne sais pas comment je peux arriver à trouver la valeur de ces 2 angles qui doivent normalement mesurer 36°, je pensais peut-être utiliser la médiatrice ?!
Merci d'avance.
J'obtiens donc :
HCB = ACB / 2
HCB = 36 / 2
HCB = 18 °
Comme HCX = 90° alors BCX = HCX - HCB
BCX = 90 - 18
BCX = 72°
Je dois donc ensuite démontrer que le point C en joignant le point I coupe l'angle BCX en 2, j'obtiendrais donc 36° soit la réponse normalement juste.
Je pense avoir trouvé la solution du 2)
Dans le triangle ADI (le point D étant la médiatrice) rectangle en D :
cos A = AD / AI
cos 72° = 5 / AI
AI = 5 / cos 72°
donc AI = 10(1 + 2cos72)
Merci.
Tu dois pouvoir déterminer la valeur des angles BCI et BIC par des calculs analogues sur les angles.
2) Où est le point D ?
Excuse-moi mais je ne vois pas ce que sont des calculs analogues 
Le point D est situé sur le segment [AC], il s'agit du point qui le coupe en son milieu et perpendiculairement.
Merci.
Ce n'est pas forcément la bonne méthode, mais en cours ils nous arrivent de le déduire directement à la calculatrice.
Salut, j ai exactement le meme exercice a rendre, je n arrive pas a deduire que la voute d ogive a pour longueur 4Pi(1+ 2cos72). Pourriez vous m aider?
Bonjours, j'ai le même exercice à faire aussi,
et il y a une chose que je comprend pas c'est comment faire pour démontrer que le point C en joignant le point I coupe l'angle BCX en 2?
Je réfléchis depuis un bon moment mais je n'ai pas trouver ...
J'éspere que quelqu'un pourra me repondre 
merci d'avance !
Pour démontrer que le triangle CIB est isocèle, tu peux déterminer la valeur des angles BIC et BCI et montrer qu'ils sont égaux.
L'angle BIC peut être calculé dans le triangle isocèle ACI.
Par ailleurs, on a BCI = ACI - ACB , ces deux derniers angles étant de valeur connue.
Enfin, l'angle ICX étant égal à l'angle BIC, la droite CI est la bissectrice de l'angle BCX.
Comment faire pour démontrer que le triangle CIB est isocèle, s'il te plait, aide-moi Priam sans tourner autour du pot car je dois rendre le DM demain à 8h 
1)
le triangle ABC est isocèle alors BCA=BAC=72
Car dans un triangle la somme des trois angle est de 180
dans un triangle isocèle les deux angle adjacent a la base sont égaux
ABT est un triangle plas il fait donc 180° car la somme de tout les angle d'un triangle est de 180°
CBA=72° 72-180=144 donc CBT=144°
si ont trace une droite(CX) paralèle a (AI)ont peut dire que cette droite est un triangle plas
la somme de tout les angle d'un triangle est de 180°
HCB = ACB / 2
HCB = 36 / 2
HCB = 18 °
Comme HCX = 90° alors BCX = HCX - HCB
BCX = 90 - 18
BCX = 72°


