Inscription / Connexion Nouveau Sujet
Exercice logarithme népérien
Bonjour, je fais appel à vous car ma professeur m'a donné un exercice faisant intervenir le lograithme népérien, mais je n'arrive pas à le résoudre et je ne sais pas du tout comment m'y prendre.
Voici l'énoncé :
Soit f la fonction définie sur l'intervalle ]0 ; +∞[ par f (x) = lnx.
Pour tout réel a strictement positif, on définit sur ]0 ; +∞[ la fonction ga par ga(x) = ax2.
On note C la courbe représentative de la fonction f et Γa celle de la fonction ga dans un repère du plan.
Etudiez l'intersection des courbes C et Γa suivant les valeurs du réel strictement positif a.
Bonjour,
Qui dit intersection dit résoudre f(x)=ga(x)
Tu pourrais étudier la fonction h(x)=f(x)-ga(x) et résoudre h(x)=0
sanantonio312 Bonjour, merci pour votre réponse. J'avais effectivement pensé à cela mais le problème c'est qu'après avoir résolu cela je ne pense pas que je pourrait savoir si la Γa coupe une ou deux fois C
le problème c'est qu'après avoir résolu cela je ne pense pas que je pourrait savoir si la Γa coupe une ou deux fois C
Qu'as-tu résolu? Qu'as-tu trouvé?
sanantonio312 Merci je m'y met maintenant et je vous communique les résultats dans quelques minutes.
Oui, mais c'est la somme de 2 fonctions continues et dérivables sur le même ensemble de définition. C'est donc immédiat.
C'est ça.
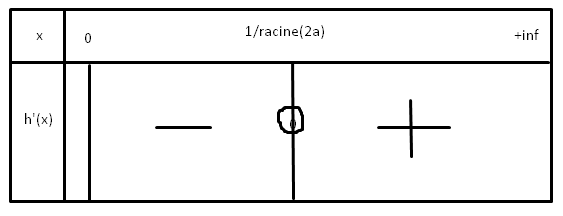
Il faut maintenant regarder les variations de h (x).
Quelles sont les limites aux bornes du domaine de définition?
Que vaut h (1/
(2a))?
L'équation h (x)=0 a-t-elle une ou des solutions?
Il manque un signe - car ln (1/z)=-ln (z)...
La question n'est pas de résoudre h(x)=0 mais plutôt d'étudier le signe de -(1/2)ln (2a)-(1/2) qui vaut aussi (-1/2)(ln (2a) + 1)
sanantonio312 Oui merci exact pour le signe il manquait un - devant premier 1/2.
Très bien, du coup j'étudie le signe du maximum ?
sanantonio312 Du coup j'en conclue que si a>1/2e alors les courbes ne se coupent pas, si a<1/2e les courbes se coupent plus de 2 fois et si a=1/2e les courbes se coupent une fois ?
Du coup j'en conclue que si a>1/2e alors les courbes ne se coupent pas, si a<1/2e les courbes se coupent exactement 2 fois et si a=1/2e les courbes se coupent une fois
sanantonio312 Mais oui je viens de comprendre ! Merci infiniment pour votre aide précieuse et votre patience ! Je vous en suis très reconnaissant !
Une fonction continue croissante de -
vers une valeur positive puis décroissante de cette valeur positive vers -.
sanantonio312 2 fois j'ai compris. Merci 
sanantonio312 Mais oui je viens de comprendre ! Merci infiniment pour votre aide précieuse et votre patience ! Je vous en suis très reconnaissant !
Annuler
connectez vous