Donc si je suis ce que vous avez dit AH = 2OA'

Non car ce sont deux vecteurs opposés

ou si l'on applique la somme de deux vecteurs cela donne et pour tout point A

D'accord mais du coup comme AO+OA= 0 et bien AH=2OA'

N'est-ce pas ce que l'on vous demandait ?

Qu'est-ce que O  ? Que peut-on dire de (OA') ?  

Bah O c'est le centre du cercle, et la droite OA'= OA ou OA'=OB ou OA'=OC

Non  Si OA=OB=OC  ce sont des rayons du cercle  A' B' et C' sont les milieux de cordes

Puisque OB =OC  que peut-on dire de O et de A'

C'est bon je viens de comprendre. Enfaite AH = AO+OA+2OA'

Aïe bah ca je sais pas parce que A' c'est le milieu du segment BC mais O c'est là où toutes les médiatrices se croises

(OA') n'est-elle donc pas la médiatrice de [BC] ?

Si c'est vrai, donc le point O c'est là ou toutes les médiatrices se rencontrent et A' est un point de la médiatrice qui coup (BC)..

J'ai compris la question b et du coup la réponse de la question c, c'est qu'on peut en conclure que (AH) et (BC) sont de même longueur car AH=2OA' et BC=2OA' aussi

Mais est-ce que on peut dire que AH=BC ? (Ils sont de même longueur certes, mais ils ne vont pas dans la même direction)

Qu'est-ce qu'une médiatrice ?

Que peut-on dire alors des droites (OA') et (AH) entre elles d'abord et par rapport à (BC) ensuite

Une médiatrice c'est une droite qui coup un segment en son milieu et qui est perpendiculaire a ce même segment

On peut dire que OA' et AH sont de même longueur

*coupe

NAAAANNN je me suis trompée AH fait 2*OA'

Non  puisque par conséquent AH=2OA' (ce sont des distances)

( OA' ) perpendiculaire à (BC)  oui

réponses à la seconde partie  (AH) est   à (OA')  donc ...

(AH) est parallèle à (OA') donc...

J'ai pas la suite

Vieux théorème :

si deux droites sont parallèles toute perpendiculaire à l'une l'est aussi à l'autre

Donc ça veut dire que (AH) est aussi perpendiculaire à [BC]  (parce que (OA') est perpendiculaire à [BC])

Voilà  et que (AH) et ( OA') sont parallèles

maintenant  vous reprenez les mêmes questions  avec B' au lieu de A' ( BH)  au lieu de (AH)

montrer que

D'accord merci beaucoup pour votre aide, est-ce que je pourrais vous renvoyer un message pour savoir si ce que j'ai fait est bon ??

Je suis les messages donc s'il y en a un nouveau je répondrai

D'accord merciii

C'est pour cela qu'il ne fallait pas répondre je sais qu'il y a un nouveau message quand le carton est jaune si non il est bleu  puisque j'ai posté en dernier

Alors voilà j'ai fini, et ça donne ça. J'ai utiliser le parallélogramme parce que je n'y arrivais pas avec Chasles...

Soit E le point défini par OE = OA + OC
Alors OAEC est un parallélogramme.
Donc ses diagonales, [OE] et [AC], se coupent en leur milieu.
Or B' est le milieu de [AC]. donc B' est le milieu de [OE].
Donc 2OB' = OE = OA + OC

Si 2OB' =OA + OC
Alors OH = OB+ 2OB'
Donc BH = BO + OB + 2OB'
             BH = 2OB'

On peut en conclure que (BH) est parallèle à (OB'), donc si deux droites sont parallèles, toute droite perpendiculaire à l'une l'est aussi à l'autre, donc (OB') est perpendiculaire à (AC), ce qui veut dire que d'après la propriété, (BH) est perpendiculaire à (AC).

Je préférerais

la première égalité vient de la construction du parallélogramme  la seconde  du fait que B' est le milieu de [OE] C'est dans cet ordre que l'on raisonne

Il faudrait préciser pourquoi les droites sont parallèles et pourquoi (OB') est perpendiculaire à (AC)

Que peut-on dire de H alors ?

D'accord je rectifierais tout ça demain et je répondrai à la dernière question comme c'est pour ma dernière heure de cour j'ai encore un petite heure devant moi. Encore merci de votre aide, sans vous je sais pas ce que j'aurais fait... 🙏🏻

Je maintiens l'utilisation de la relation de Chasles pour la première question est beaucoup plus simple
Il doit manquer des questions car il n'a pas été question du centre de gravité

La droite d'Euler est la droite passant par l'orthocentre le centre de gravité et le centre du cercle circonscrit  autrement dit G Oet H alignés
De rien

Euh oui 😅 il y avait la suite, mais elle est en rapport avec la partie c du premier exercice, et je ne comprenais pas cette partie donc je me suis dit que c'est pas grave 😅

Je m'étonnais juste qu'on ne s'occupait pas de l'alignement des 3 points. Si vous avez pu répodre aux questions c'est très bien

Alors nan enfaite dans l'exercice 1 il y a 3 partie A, B et C, et j'ai fait la A et la B mais je n'ai pas compris la C. Et c'est en faisant le deuxième exercice (dedans il y a la partie 1, celle que vous m'avez aider à faire, et la partie 2) que je me suis rendue compte que la partie 2 est en rapport avec la partie C du premier exercice...

Si vous avez besoin d'aide en rapport avec cet exercice  venez poser vos questions  ici mais avec un autre exercice il faudra ouvrir un autre sujet

D'accord, et bien voici l'énoncé :

On appelle G le point d'intersection des médianes.
1) Prouver en utilisant G' le symétrique de G par rapport à A' que AG=AA' (remarquer que CGBG' est un parallélogramme et utiliser Thalès ou le théorème de la droite des milieux)
2) Prouver enfin que GA+GB+GC=0 et que quel que soit le point O du plan, OG=(OA+OB+OC)

Ce sont des vecteurs...

Le point G ainsi défini est appelé centre de gravité du triangle ABC.

J'ai oublier la dernière phrase

Que peut-on dire du quadrilatère GBG'C ?

Des droites et

Que savez-vous sur la droite des milieux  ?

Les réponses sont meilleures sur Math-Forum ?

Non c'est juste que vous mettiez du temps à répondre donc je pensais que vous en aviez marre de m'aider parce que je comprenais pas.
J'ai pas pu finir mon DM avec ce que vous avez donner comme piste j'ai du le rendre mais merci quand même, grâce à vous j'ai pu comprendre des choses que je n'avais pas compris avec mon professeur de maths...

Je ne pense pas avoir trop tardé à vous répondre
Si j'arrête je le dis  
La prochaine fois  écrivez le texte en entier  et précisez davantage les questions où vous bloquez.

Rapidement   en utilisant la droite des milieux vous montrez que G est le milieu de [AG']

puis GA'= 1/2GG'

et on réutilise c'est pour cela aussi que j'insistais dans votre première question à utiliser les vecteurs

On peut même considérer comme un théorème

I est le milieu de [AB] si et seulement si  pour tous points et

Et quel est le rapport avec la droite d'Eluer

Euler

On vous guidait   Toujours même principe





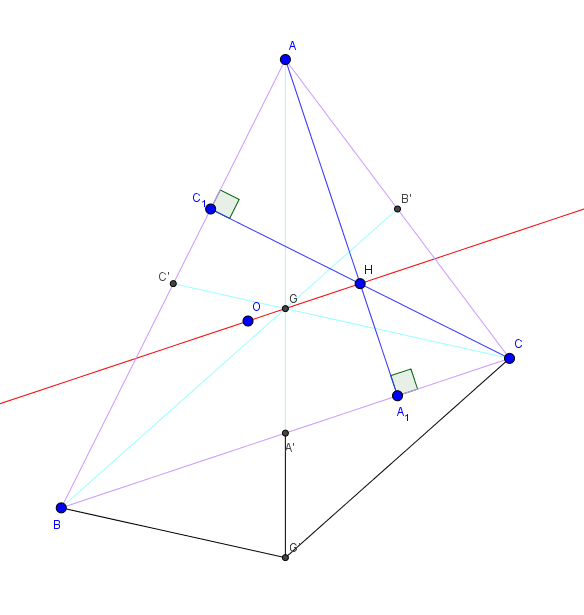
Les points O, G et H sont alignés.  La droite passant par ces trois points est la droite d'Euler

D'accord merci 😊

De rien

Bonsoir,

C'est la droite d'Euler !
Euler : mathématicien suisse