Inscription / Connexion Nouveau Sujet
Exercice sur la droite d'Eluer
Bonjour,
J'ai un DM à rendre pour demain que j'ai commencé a faire pendant les vacances mais la il me reste juste cette après-midi pour je faire et je bloque complètement sur le dernier exercice :
Soit ABC un triangle quelconque.
Soit A', B', C' les milieux respectifs des coté [BC], [AC] et [AB].
On note O le centre du cercle circonscrit au triangle ABC,
G son centre de gravité et H le point tel que :
OH = OA + OB + OC
Le but de cet exercice est de démontrer que les points O, G et H sont alignés.
a. Démontrer que OB + OC = 2OA'
b. En déduire l'expression de vecteur AH en fonction du vecteur OA'.
c. Que peut-on conclure pour les droites (AH) et (BC) ?
d. Démontrer de même que la droite (BH) est perpendiculaire à la droite (AC).
e. Que représente le point H pour le triangle ABC ?
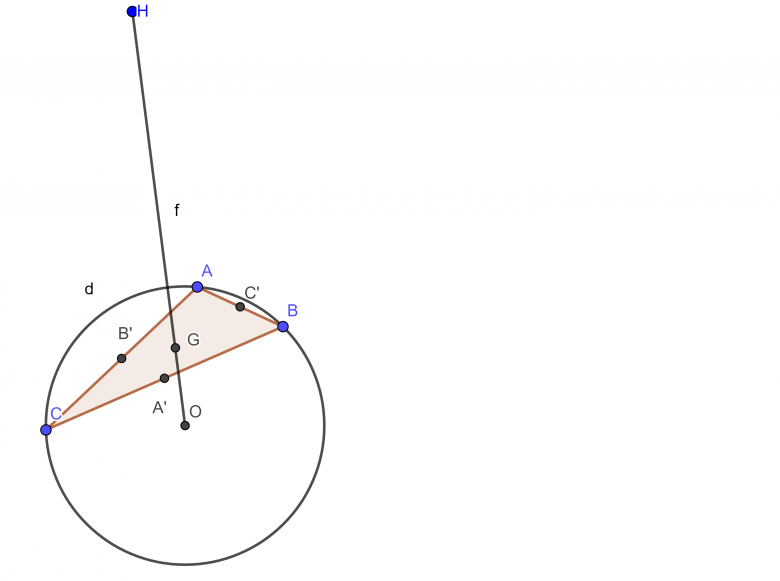
Voilà mon exercice, ce qui est en italique et gras ce sont des vecteurs, j'ai représenté la figure sur geogebra et je l'ai rattacher a mon poste. Pouvez-vous m'aider s'il vous plait 
a) imagine le parallélogramme OBCD avec D à construire. Comment se coupent les diagonales d'un parallélogramme ?
b) utiliser la définition de H dans a)
c) Quelle est l'intersection des médiatrices d'un triangle ?
d) Tout est symétrique en A,B,C
e) Regarde c'est que l'orthocentre d'un triangle
Conclusion : regarde ce qu'est la droite d'Euler d'un triangle
Mais tu as internet à ta disposition 
Ce sont des noms pas forcément vus en classe, mais les résultats devraient être accessibles pour un élève de lycée.
Et le fait que les diagonales d'un parallélogramme se coupent en leur milieu ne va rien m'apporter de plus pour répondre à ma question... -_-
Pour la première question il n'y a besoin que de la relation de Chasles
Ici on a introduit le point B
faites de même en introduisant le point A'
Je te donne des indications, pas la solution.
Dans un parallélogramme EFGH, tu as toujours
Les relations de Chasles fonctionnent aussi, effectivement (j'ai l'impression ce que je propose se voit un peu mieux sur le dessin, mais ça reste personnel).
Ooohhh je viens de comprendre, si je forme le parallélogramme OBCD (comme vous l'avez dit précédemment),
OBCD est un parallélogramme ssi OB = CD
ssi OC = OB + OD
Si I milieu de OC : OI = 1/2OC
OI = 1/2OC
OBCD parallélogramme ssi{
BI = 1/2BD
Donc : OB = BO u ssi -u
u ssi ku
k
0
Ou bien c'est pas du tout ça et je me suis complètement tromper °-°'
On ne parle pas de coordonnées
Juste la relation de Chasles et oui il faudra utiliser le fait que A' est le milieu de [BC]
Le problème de frappe c'est pas grave ça peut se réglé, merci beaucoup à vous deux j'ai compris la question a 
Et je voulais savoir si c'était bon ou si il y avait des choses à changer ou a rajouter...
OBDC est un parallélogramme ssi OB = DC
ssi OD = OB + OC
Si A' milieu de OD : OA' = 1/2OD
OA' = 1/2OD
OBCD parallélogramme ssi{
BA' = 1/2BC
Donc A' est le milieu du parallélogramme OBDC.
C'est assez étrangement rédigé. Qu'est-ce que le milieu d'un parallélogramme ?
Tu as compris l'idée, donc je vais le rédiger pour ne pas y passer trop de temps.
Soit D le point défini par OD = OB + OC
Alors OBDC est un parallélogramme.
Donc ses diagonales, [OD] et [BC], se coupent en leur milieu.
Or A' est le milieu de [BC]. Donc A' est le milieu de [OD]
Donc 2OA' = OD = OB + OC
Donc AH = OA + OB parce que OH = OA + OB + OC et AH = OH-1 Fin je sais pas trop comment dire... mais du coup AH = 2OA
D'accord, je n'avais pas d'exemple de rédaction, et l'année dernière la leçon sur les vecteurs on devait la faire pendant le confinement mais on a jamais eu de leçon bref merciii et du coup je pense que ma réponse de dessus est juste...
Ouais, Chasles est assez sympa pour la a) hekla
C'est simplement une deuxième méthode, à toi de voir celle que tu comprends le mieux.
Pour bae14, utilise AH = AO + OH puis utilise a)
C'est une question de point de vue, personnellement le Chasles je le trouve sorti du chapeau, alors que sur le dessin introduire le parallélogramme me semble assez naturel
Au moins ça donne deux intuitions d'un même problème. Et si ça permet de mieux comprendre ce qu'il se passe, pourquoi pas...
Pour bae14, utilise AH = AO + OH puis utilise a)
AH ne peut pas être égale à AO + OH parce que AO + OH est plus grand que AH
Au lieux d'écrire on choisit d'écrire AB, parce que c'est plus rapide au clavier.
Si ça t'induit en erreur, on peut revenir aux flèches, ou en gras
Le dessin est fait pour ne pas se perdre avec les lettres, si tu as un doute sur ce qu'il se passe regarde le dessin
Vous n'avez jamais entendu parler de la relation de Chasles Ou comment additionne-t-on deux vecteurs ?
Je me repère avec le dessin, mais enfaite je me perds parce que je comprends pas comment AH = AO + OH
Et nan je me souviens pas avoir appris la relation de chasles...
Prends 3 points A,B et C. Tu vois que c'est la même chose d'aller de A à B directement ou de A à C puis de C à B : on arrive au même point.
En écrivant ça avec des vecteurs, ça donne la relation de Chasles :
AH = 2OA'
Parce que il est demander en fonction du vecteur OA' et on sait que 2OA'= OD = OB+OC
Et O étant le centre du cercle, OA est le rayon donc comme OB + OC = 2OA', AH = 2OA'
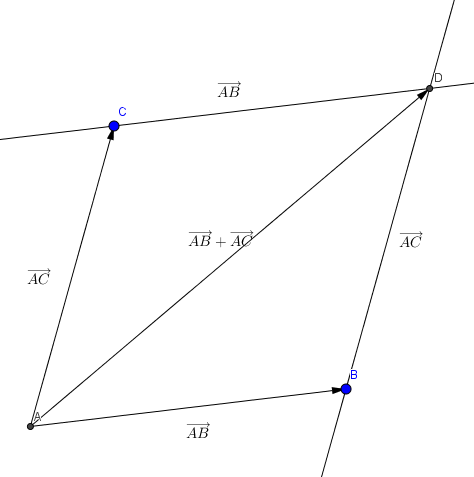
Construction de la somme de deux vecteurs
On dit que } est la somme des vecteurs
et
Le quadrilatère ABDC est un parallélogramme si et seulement si
est la relation de Chasles
Voir ici sur les vecteurs ![]() Vecteurs
Vecteurs
On te donne des indications, pas la solution ,c'est à toi de travailler un peu.
Utilise la question a)


