Inscription / Connexion Nouveau Sujet
Exercice sur la fonction logarithme
Bonjour à tous !
J'ai un soucis avec une étude de fonctions, si vous pouviez m'aider se serait super.
Voici l'énoncé.
A. Soit f la fonction définie sur  par :
par :
f(x) = 2e2x - ex
e2x - ex + 1
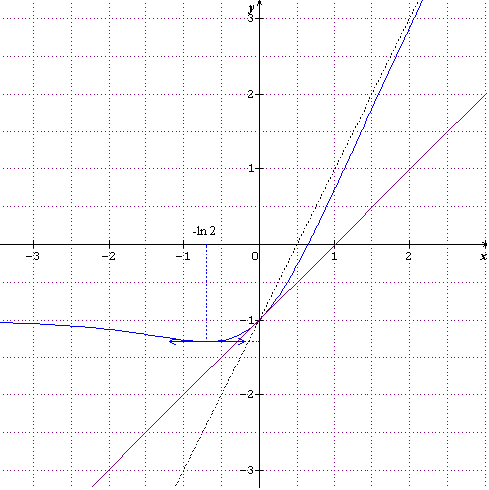
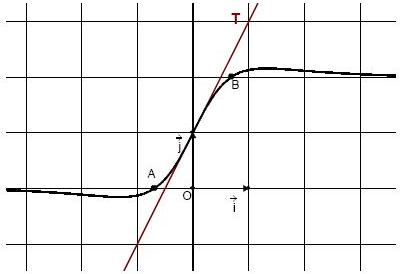
On donne la courbe Cf représentative de f dans un repère orthonormé (O,  ,
,  ) du plan. (La courbe représentative se trouve à la fin de mon message)
) du plan. (La courbe représentative se trouve à la fin de mon message)
Le point I de coordonnées (0 ; 1) est un centre de symétrie de Cf et la droite T est tangente à Cf en ce point.
1. a. Étudier la limite de f en - ∞ et en + ∞.
Interpréter graphiquement les résultats.
b. Calculer l'abscisse du point d'intersection, noté A, de Cf et de l'axe des abscisses.
En déduire l'abscisse du point B de Cf d'ordonnée 2.
2. On répondra aux questions suivantes grâce à une
lecture graphique et sans aucun calcul.
a. Donner le signe de f sur  .
.
b. Donner la valeur de f'(0)
3. Déterminer la primitive G sur  de f qui prend la
de f qui prend la
valeur -1 en 0.
B. Soit F la fonction définie sur  par :
par :
F(x) = ln ( e2x - ex + 1) - 1
et  sa courbe représentative dans le repère (O,
sa courbe représentative dans le repère (O,  ,
, ).
).
1. a. Étudier la limite de F en - ∞.
Interpréter graphiquement le résultat.
b. Démontrer que :
Pour tout réel x, F(x) = 2x + 1 +ln ( 1 - e-x) + e-2x).
c. Étudier la limite de F en + ∞.
d. Démontrer que la courbe  admet une asymptote oblique d'équation y=2 x - 1 en + ∞.
admet une asymptote oblique d'équation y=2 x - 1 en + ∞.
2. Déduire de la partie A le sens de variation de F et
dresser son tableau de variation.
3. Tracer la courbe et ses asymptotes ainsi que la droite tangente à
et ses asymptotes ainsi que la droite tangente à  au point d'abscisse 0.
au point d'abscisse 0.
J'ai réussi à faire la question 1. a) j'ai donc trouver :
lim f(x) = 2 en +  et 0 en -
et 0 en -  , il y a donc 2 asymptotes verticales y = 2 en +
, il y a donc 2 asymptotes verticales y = 2 en +  et y = 0 en -
et y = 0 en - 
Pour la question 1. b) j'ai résolu f(x) = 0 mais je trouve x = 0 ce qui n'est pas cohérent avec le dessin qui m'ai donné
Pour la question 2. a) j'ai répondu pour x ]-
]-  ; A] f(x)
; A] f(x)  0 et pour x
0 et pour x  [ A; +
[ A; +  [ f(x)
[ f(x)  0
0
Pour la question 3. j'ai cherché la primitive de f qui répond à la condition f(0) = 1 mais je ne sais pas comment faire la primitive d'un quotient d'exponentielles.
Merci d'avance pour votre aide.
Bonne journée !
Bonjour,
Si ta fonction est bien définie par alors :
1a) tes limites sont justes mais ce sont des asymptotes horizontales et non pas verticales bien sûr...
1b)l'équation f(x)=0 équivaut successivement à :
2e2x-ex=0
ex(2ex-1)=0
ex=0 ou ex=1/2
or pour tout réel x, ex>0
donc on obtient ex=1/2 donc x=ln(1/2) ou encore x=-ln(2)
Pour la question 2a) il faut remplacer A par son abscisse (qu'on vient de trouver à la question 1b) )
Bonjour !
merci beaucoup pour votre aide !
Ma fonction est bien celle que vous avez écrite, le problème c'est que je ne savais pas comment l'écrire sous cette forme.
Pour la question 1.a) j'avais bien écrit horizontale sur mon brouillon...
Et la question 1.b) je m'obstinais à vouloir garder le dénominateur à tout prix, alors que pourtant je savais le faire...
Pour trouver l'abscisse du point B de Cf d'ordonnée 2 j'ai trouvé:
x = ln(1 -  17) (l'autre solution étant négative)
17) (l'autre solution étant négative)
4
Pour la question 2.a) c'est bon.
Je cherche pour la 2.b) et la 3. je suis plus motivée que tout à l'heure, merci beaucoup !!
Pour la 2.b) je pense que la valeur de f'(0) c'est le coefficient directeur de la tangente en 0, soit 2. C'est bon ?
Oui, f'(0) est bien égal à 2. 
Mais pour l'abscisse du point B, moi je trouve ln(2) tout simplement...
Pour l'abscisse du point B j'ai fais n'importe quoi, je trouve bien ln(2) en le refaisant correctement.
Pour la primitive j'ai quelquechose sous la forme de u'(x)
un(x)
Le problème c'est que n vaut 1, donc (n-1) dans la formule de la primitive fait 0... ou sinon je dis que c'est (1/x)' = ln (x) ce qui donne G(x)= ln(e2x-ex+1) + k qui est le résultat de la partie B.
Ensuite en utilisant G(0)=-1 je trouve k = -1
donc la primitive G de f qui prend la valeur -1 en 0 est G(x) = ln(e2x-ex+1) - 1.
je ne sais pas trop comment rédiger pour la première partie avec (1/x)' = ln (x) puisque ce que ce n'estpas exactement ce que j'ai...
f est une fonction de la forme u'/u avec u(x)=e2x-ex+1>0
Donc les primitives de f sont les fonction de la forme F=ln(u)+k
Pour trouver LA primitive de f qui prend la valeur -1 en 0 il faut déterminer k tel que G(0)=-1...
Bonjour,
J'ai commencé la partie B.
Question 1a)
lim F(x) = -1 quanq x tend vers -
car si on pose X = e2x - ex + 1
lim X = 1 quand X tend vers -
or ln (1) = 0
donc lim F(x) = -1 quanq x tend vers -
Donc il y a une asymptote horizontale d'équation y = -1 en -
Est-ce que ma rédaction est bonne ?
J'ai réussi à démontrer la question 1b)
Pour la question 1c) j'ai :
lim F(x) = +  car
car
si on pose X = e2x - ex + 1
on a lim X = +  quand x tend vers +
quand x tend vers +
donc lim ln X = + quand X tend vers +
quand X tend vers +
Pour la question 1d)
J'ai démontré que lim (F(x) - (2x - 1)) quand x tend vers +  = 0
= 0
si on pose X = 1 - e-x + e-2x
on a lim X = 1 quand x tend vers + 
or ln(1) = 0
donc y = 2x - 1 est asymptote oblique à la courbe en +
Pour la question 2)
f(x) est la dérivée de F(x) donc de là on en déduit ses variations :
Pour x  ]-
]- ; ln(2) [ F est strictement décroissante
; ln(2) [ F est strictement décroissante
Pour x  ] ln(2) ; +
] ln(2) ; +  [ F est strictement croissante
[ F est strictement croissante
Pour la question 3)
J'ai un problème pour tracer la tangente au point d'abscisse 0, est ce qu'il faut calculer son coefficient directeur ou je la trace juste en suivant la courbe le mieux possible ?
Merci d'avance pour votre aide
Bonjour,
Tes réponses sont presques toutes correctes... je préciserais seulement que :
pour la question 1c) il aurait été plus simple d'utiliser la forme F(x)=2x-1+ln(1-e-x+e2x)
Pour la question 2, petite erreur de signe :
Pour x ]-
]- ;-ln2] f(x)<0 donc F est décroissante sur cet intervalle,
;-ln2] f(x)<0 donc F est décroissante sur cet intervalle,
pour x [-ln2;+
[-ln2;+ [, f(x)>0 donc F est croissante sur cet intervalle.
[, f(x)>0 donc F est croissante sur cet intervalle.
Pour la question 3, on sait que f(0)=1. Donc le coefficient directeur de la tangente à  est 1.
est 1.
Voici le dessin en prime