Soit ABC un triangle équilatéral direct et i le milieu du segment [BC].
Le but de l'exercice est de déterminer l'ensemble E des points M du plan tels que :
(vecteur IM, vecteur AB)=-(2pi)/3

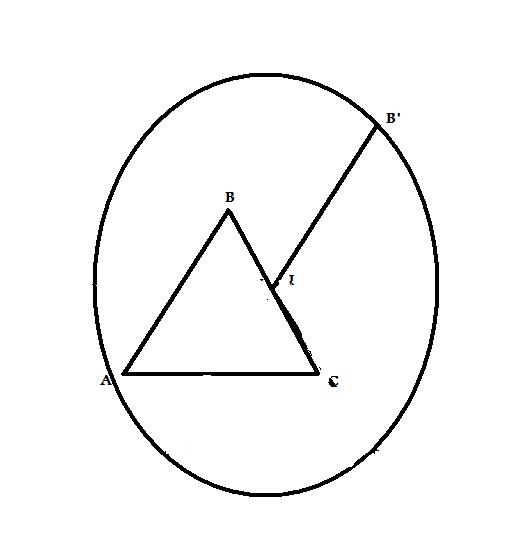
1) Faire une figure illustrant la configuration et placer le point B' tel que vecteur IB'= vecteur AB.

2) Démontrer que le point C appartient à l'ensemble E.
Le point B' appartient-il à E ?

3) Démontrer que M appartient à l'ensemble E si et seulement si (vecteur IM, vecteur IC)= 0

4) En déduire l'ensemble E.

Pouvez vous m'aider pour cet exercice s'il vous plait, je ne sais meme pas par ou commencer...