Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Angles orientésTopics traitant de angles orientés [tout]Lister tous les topics de mathématiques

1 2 3 +

Niveau première
Partager :

exercice sur les angles orientés

Posté par
miss-rock 18-04-10 à 20:40

Bonsoir,

J'ai un DM de maths à faire et je bloque sur un exercice.
En voici l'énoncé :

Dans le plan orienté muni d'un repère orthonormé direct (O ; ; ), on considère les points A de coordonnées (2;1) et B de coordonnées (1/2 ; 1+(3/2)).

1) Calculer les coordonnées du vecteur AB.

2) Soit une mesure, en radian, de l'angle orienté (;AB). Calculer cos et sin.
En déduire une mesure de l'angle (;AB).

3) Soit x un réel de [5;11/2) tel que cos x = (-1)/2.
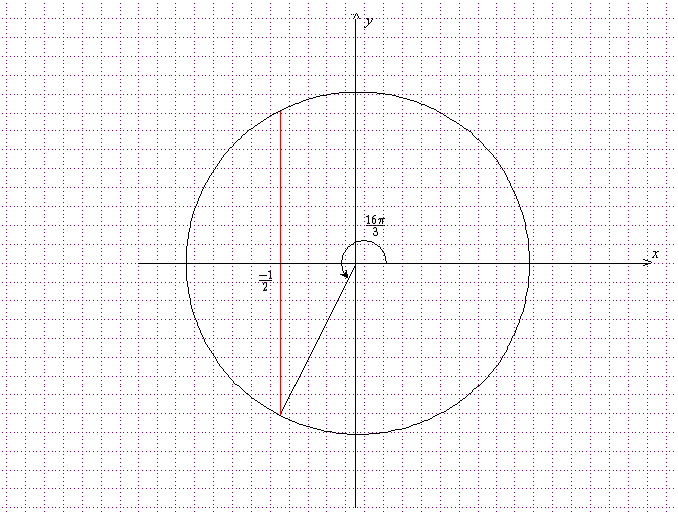
  a) Placer le point M image de x sur le cercle trigonométrique de centre O et calculer sin x.
  b) Trouver x.

4) Montrer que les droites (OM) et (AB) sont perpendiculaires.

Est-ce que quelqu'un pourrait m'aider s'il vous plaît ?

Merci d'avance.

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 20:43

Pour la première question, j'ai trouvé AB ( (-3)/2 ; (3)/2 ).

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:27

3$\rm Bonsoir,\\Je suis d^,accord pour les coordonne^,es du vecteur \vec{AB}\\pour la 2e^,me question il faut calculer le produit scalaire \vec{i}.\vec{AB}:\\\vec{i}.\vec{AB}=||\vec{i}||.||\vec{AB}||cos(\vec{i},\vec{AB})

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 21:36

Mais on ne connaît pas assez de données pour appliquer cette formule
La longueur de est 1 ? car on est dans un cercle trigonométrique.
Mais on connaît pas le reste.

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:40

3$\rm Si si on connais tout ou presque!

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 21:44

Euh je vois pas du tout, on en connaît pas la norme de AB et encore moins le cosinus

Pourriez-vous m'éclairer s'il vous plaît ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:45

3$\rm pour le vecteur \vec{i} je suis d^,accord les coordonne^,es sont (1; 0)\\tu viens de trouver les coordonne^,es du \vec{AB} qui sont :\\(-\frac{3}{2} ; \frac{\sqrt{3}}{2})\\avec ceci tu sauras calculer leur norme?

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 21:51

Je suis désolée mais je ne sais pas faire

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:52

3$\rm Je vois tu es en premie^,re alors vous n^,allez pas tarer a^, les fair en cours

3$\rm il faut que tu saches que le produit scalaire de 2 vecteurs est :\\\vec{u}.\vec{v}=||\vec{u}||.||\vec{v}||cos(\vec{u} ; \vec{v})

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 21:55

Oui d'accord.

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:56

3$\rm ||\vec{i}||=\sqrt{1^2+0}=1\\||\vec{AB}||=\sqrt{(-\frac{3}{2})^2+(\frac{\sqrt{3}}{2})^2}=\sqrt{3}

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 21:58

Vous avez calculer les normes là ?

D'où est-ce que ça sort ? C'est quelle formule ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 21:59

3$\rm il reste a^, faire le produit scalaire \vec{i}.\vec{AB}=1\times(-\frac{3}{2})+0\times(-\frac{3}{2})= -\frac{3}{2}

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:01

3$\rm le norme d^,un vecteur de coordonne^,es \vec{u}(a;b)\\||\vec{u}||=\sqrt{a^2+b^2} c^,est la de^,finition

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:02

Mais là vous n'avez pas utilisé la formule que vous aviez dit au début.

Et ce n'est pas 03/2 ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:03

3$\rm Si si c^,e^,tait le produit scalaire et non pas la norme

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:04

Mais dans le produit scalaire, il n'y a pas d'addition

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:06

3$\rm Si si Soient \vec{u}(a,b)~,~\vec{v}(c,d)\\\vec{u}.\vec{v}=ac+bd

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:07

Ah d'accord désolée.

Mais que faut-il faire avec le produit scalaire ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:12

3$\rm re^,capitulons Nous avons la formule qu^,on connait:\\\vec{i}.\vec{AB}= ||\vec{i}|| .||\vec{AB}||cos(\vec{i} ; \vec{AB})

3$\rm Connaissant \vec{i}.\vec{AB}=-\frac{3}{2}\\||\vec{i}||=1\\||\vec{AB}||=\sqrt{3}

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:14

3$\rm il ne te reste plus qu^a^, calculer cos(\vec{i} ; \vec{AB})

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:15

Ah d'accord parfait, merci.

En faisant ça, j'ai obtenu cos (;AB) = (-3)/23.

Et à la calculatrice, j'ai trouvé 150.

Est-ce que c'est juste ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:16

3$\rm pas mal

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:16

Cela veut-dire que c'est juste alors ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:17

3\rm non c^,est pas cela tu vas trop vite!

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:19

Ah bon

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:22

3$\rm il faut faire calmement ce calcul :\\cos(\vec{i} ; \vec{AB})=\frac{\vec{i}.\vec{AB}}{||\vec{i}|| .||\vec{AB}||}=\frac{-\frac{3}{2}}{1\times(\sqrt{3})}=-\frac{\sqrt{3}}{2}\\tu n^,as pas besoin de calculatrice !

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:25

Mais après j'ai fait : -3/2 1/13 et j'ai trouvé  -3/23.

Et j'ai utilisé la calculatrice pour faire cos-1 (-3/23).

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:27

3$\rm je n^,ai pas dis que c^,est faux mais que tu vas trop vite\\-\frac{\sqrt{3}}{2} est le cosinus d^,un angle remarquable que tu dois connaitre

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:31

C'est soit 5/6 soit -5/6, non ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:37

3$\rm exact et pour savoir lequel des 2 on te demande le sinus justement

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:40

Le sinus c'est soit 1/2 soit -1/2.

Comment sait-on lequel sait ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:44

3$\rm alors la^, je suis pas sur que ma me^,thode puisse te convenir\\puisque elle fait appelle au produit vectoriel\\je ne sait plus comment on faisait en premie^,re

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:45

Ah ok.

Mais tu peux m'expliquer quand même s'il te plaît ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:47

3$\rm oui bien sur attent un peu cette me^thode fait appelle au produit vectoriel et non le produit scalaire

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 22:55

D'accord, merci.

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 22:56

3$\rm attends je redige

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 23:05

3$\rm en tout cas je mets ma solution :\\sin(\vec{i} ; \vec{AB})=\frac{\vec{i}\wedge\vec{AB}}{ ||\vec{i}||.||\vec{AB}|| }

3$\rm ce machin \wedge~~(un V retourne^,) est le signe du produit vectoriel

3$\rm {\vec{i}\wedge\vec{AB}} = 1\times\frac{\sqrt{3}}{2}-0\times(-\frac{3}{2})=\frac{\sqrt{3}}{2} \vec{k}\\||\vec{i}||.||\vec{AB}|| de^,ja^, calcule^,\\||\vec{i}||.||\vec{AB}||=-\frac{3}{2}\\sin(\vec{i} ; \vec{AB} )=\frac{\frac{\sqrt{3}}{2}}{\sqrt{3}} \vec{k}=\frac{1}{2}\vec{k}\\donc le sinus est positif parconse^,quent\\(\vec{i} ; \vec{AB})=\frac{5\pi}{6}

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 23:08

Euh oui, et bien merci beaucoup.

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 23:15

Pourrais-tu encore m'aider pour les deux dernières questions s'il te plaît ?

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 23:18

3$\rm j^,ai marque^, ||\vec{i}||.||\vec{AB}||=-\frac{3}{2}\\je me suis trompe^, ||\vec{i}||.||\vec{AB}||=\sqrt{3} sinon mon re^,sultat est juste car j^,ai bien \\mis \sqrt{3} au nume^,rateur dans mes calculs

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 23:19

3$\rm tu ne veux pas continuer demain?

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 23:19

Ah oui en effet.

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 23:19

Euh si d'accord.

Merci pour tout.

Posté par
camillemre : exercice sur les angles orientés 18-04-10 à 23:20

3$\rm Bonne nuit a^, demain

Posté par
miss-rockexercice sur les angles orientés 18-04-10 à 23:21

Bonne nuit à toi aussi.

Merci encore.

A demain.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 16:35

3$\rm Bonjour,\\Pour la deuxie^,me question je mets la fig pour mieux comprendre\\essaye de faire tu me fais signe de^,s que tu as fini

exercice sur les angles orientés

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 19:59

Bonsoir,

Il faut déjà placer le point x, il faut juste le placer sur -1/2 ? Sans rien faire d'autre ?

Et le point M est à l'opposé de x ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 20:58

3$\rm x est un angle et non un point x=\frac{16\pi}{3}

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 21:00

Ah d'accord ok merci.

Mais alors le point M est l'intersection du rayon que tu as tracé et du cercle ?

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !