Bonjour

Je ne sais pas pourquoi je bloquais totalement sur la dérivée de g. Mais je viens de trouver -4/x². C'est bien ça ?

Du coup pour la suite
g'(2) = -4/2² = -1

y= -1(x-2)+3
y= -1x+2+3
y= -x+5
C'est juste ?

Donc je peux dire pour la c. que l'équation de la tangente T à Cf au point A et la même que celle de la tangente T' à Cg au point B

je n'ai pas vérifié tes calculs
mais dérivée de g OK cette fois
donc si tu trouves la même chose, c'est tout bon !
bonne journée !

Merci  pour votre aide !

Il y a une suite à cet exercice. Voici l'énoncé :
"2) a. Étudier la position de la courbe Cf par rapport à T sur l'intervalle ]0;+[.
b. Étudier la position de la courbe Cg par rapport à T' sur l'intervalle ]0;+[."

Il me semble bien qu'on a vu comment le faire mais je ne m'en rappelle pas du tout :/

tu dois étudier le signe de la différence f(x)-y (où y représente l'ordonnée d'un point de la tangente)

Je dois calculer ceci :
f(x)-y= -x²+3x+1-(-x+5)
= -x²+4x-4
?

oui, mets - en facteur
puis signe évident....

Mettre - en facteur, c'est à dire ?

ben mets -1 en facteur....

C'est à dire faire ceci : f(x) = -1(x²-4x-4) ?

oui, puis ouvre tes yeux !....moi je vois une belle identité remarquable !

Ah oui en effet ! Mais si je trouve (x-2)² = x²-2*2x*+2² alors ce n'est pas égal à x2-4x-4 à cause du signe de -4 à la fin

parce que tu t'es trompé en mettant -1 en facteur !! (je ne l'avais pas vu, excuse, mon cerveau avait rectifié ! )

Ah oui d'accord et moi je fais une erreur mais je m'en rends même pas compte ^^

Donc, partant du constat de l'identité remarquable -1(x-2)² = 1(x²-2*2x+2²) = -1(x²-4x+4) que dois-je faire ensuite ? Trouver le signe ?

oui, trouver le signe de -1(x-2)²

C'est toujours négatif ?

oui ! et nul pour x=2
tout simple ....

Pour le "prouver" dans ma copie, je dois faire comment ?

ben un carré ! tu connais son signe !

Je me suis embrouillée toute seule, tout va bien en fait

Bon du coup la suite :
2)b. g(x)-y = 4/x+1-(-x+5)
=4/x+1+x-5
=4/x+x-4
Est-ce que je peux aller plus loin ?

réduction au même dénominateur et étude du signe du quotient

Je continue donc...
=4/x+x²/x-4x/x
=(x²-4x+4)x

Là c'est négatif sur ]-;0[ et positif sur ]0;+[ mais comment je peux le prouver ? (je me suis servie de ma calculatrice pour trouver ça)

eh bien tu as encore une identité remarquable au numérateu....

C'est x(x-4) toujours mais là pour le signe je sais pas

=(x²-4x+4)/x =(x-2)²/4
non ?

Oula j'avais écrit n'importe quoi. Je voulais dire (x-2)²/x

Comment se fait-il que le 4 passe en dénominateur à la place du x, qui disparait ?

j'ai écrit n'importe quoi ! excuse..._{.(je me dépĉhe de répondre à tous les messages...)}
(x-2)²/x

C'est donc  négatif sur ]-;0[ et positif sur ]0;+[ mais comment je le prouve sur ma copie ?

comme tu l'as trouvé !!
le numérateur est toujours positif
donc ta fraction a le même signe que ton dénominateur

D'accord, tout simplement !

Il reste encore une question à cet exercice mais je vais essayer de la résoudre seule cette fois ci

En attendant merci beaucoup pour vos réponses et votre aide !

ok, si tu es ennuyé(e), tu posteras à la suite ici, mais essaie de la faire seul(e), c'est mieux !

Oh en fait juste une dernière question !

En fait ça veut dire quoi vraiment "étudier la position de la courbe Cf par rapport  à T sur un ]0;+[" ? Parce que c'est juste une tangente en fait, donc c'est une droite qui touche la courbe un point, et du coup je vois pas en quoi il y a une position particulière. C'est si elle est concave, convexe ?

étudier la position, c'est dire si la courbe est au dessus ou en dessous de la tangente

D'accord ! Ça m'étonne que le prof nous ai pas demandé la convexité du coup mais bon

Petite question de dernière minute :
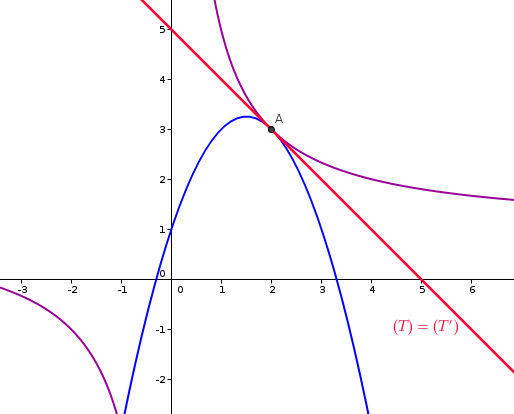
Pour la question suivante je dois tracer les droite T et T'
Or elles ont la même équation, donc sur le graphique on voit une seule droite.
Comment faire pour la nomination ?

Et pour une droite "en deux parties" (nulle en 0), je dois écrire son nom sur les deux parties ou une seule suffit ?

tu mets (T)=(T') à côté de ta droite

Merci !