Inscription / Connexion Nouveau Sujet
Exercice trigonométrie
Bonjour, j'ai un problème avec un exercice, on me demande de résoudre un triangle rectangle en A avec a(=hypoténuse)=322.45m et AH(=h)=143.35.
J'ai trouvé que dans AHC sinc=h/b et que dans ABC sinc=c/a
Donc h/b=c/a=sinc et h*a=b*c ou (h*a)/c=b
Avec a²=b²+c²
a²=(h²*a²)/c²+c²
Soit c^4-a²*c²+h²*a²=0
Avec C=c² on a;
C²-a²*C+h²*a²=0 équation 2nd degré
 =b²-4ac
=b²-4ac
avec a=1 , b=a² , c=h²*a²
b=a²=103974.0025
c=h²*a²=2136584911.58805625
 =103974.0025²-4*1*2136584911.588
=103974.0025²-4*1*2136584911.588
= 2260482061.110228

 =47544.53
=47544.53
comme  est positif il existe deux solutions
est positif il existe deux solutions
x1=(-b-
 )/2a
)/2a
x2=(-b+
 )/2a
)/2a
Dans les deux cas je tombe sur un resultat négatif ce qui est impossible dans cet exercice, je doit faire une erreur quelque part)
Pouvez vous m'aider?
Merci
Merci pour ta réponse,
je ne suis pas sur de bien comprendre, b=-a²=-103974.0025 c'est bien ça?
La effectivement j'aurais pour x1; -b-
 /2a
/2a
=(103944.002-47544.53)/2 = 28199.736 pour c²
Donc c= 28199.736=167.93
28199.736=167.93
Juste?
Bonsoir ,
sans trigonométrie
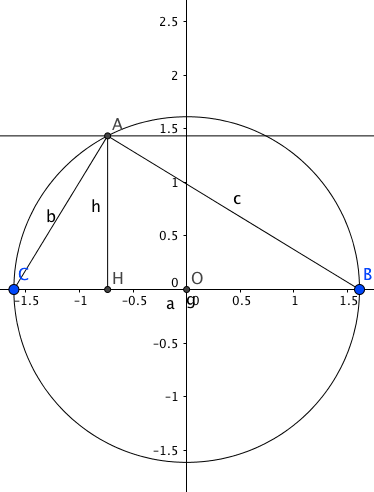
le triangle ABC est inscrit dans le cercle de diamètre [BC]
en posant B(-a/2;0 ) C(a/2;0)
équation du cercle circonscrit au triangle
or A (x,h)
b=AC
c=BC
Je ne connais pas les formules sur les cercles circonscrit au triangle mais effectivement cela me semble plus rapide.
Après avoir trouver les deux valeurs de c j'utilise Pythagore pour trouver deux valeurs de b. Puis les règles avec les sin/cos/tg pour les angles. Comment es-ce que je peu savoir laquelle des deux valeurs pour b et c est juste?
Pour revenir à l'équation C² - a²C + h²a² = 0 , on voit que la somme et le produit de ses solutions sont positifs, de sorte que les deux solutions sont positives.
Comment peux-tu alors trouver une solution négative ?
Donc, comment es-ce que je fini mon exercice avec deux valeurs possible pour les longueurs c et donc b?
pardon j'ai écrit un "comment" de trop
Es-ce que je doit finir mon exercice avec deux valeurs possible pour les longueur b et c ?
Oui, valeur possible pour b=167.93 ou b=275.23
c=275.27 ou c=167.99
Donc (l'angle) C=58.60° ou C=31.39°
B=31.38° ou B=58.60°
Je trouve pour S=1/2*ah=23111.6m² (calcul avec a et h données fournies dans l'énoncé)
Pour S=1/2bc=23113.04m² soit =23117.94m²
Cela me paraît parfait.
Le calcul donne les valeurs de b et c , ou de c et b . Il y a en effet deux triangles répondant aux conditions fixées, symétriques par rapport à l'axe Oy.


 en terminale
en terminale