Inscription / Connexion Nouveau Sujet
Exercice Trigonométrie
Salut tout le monde, j'ai un exercice à faire pour demain mais j'ai du mal. Merci de m'aider 
On donne la fonction f définie sur R par f(x)= 1 - 8cos(x) - 4cos(2x)
1) Expliquer pourquoi il suffit d'étudier f sur l'intervalle [0;
]
2) Calculer f'(x) et vérifier que son signe est celui de 1 + 2cos(x) sur [0;]; en déduire le tableau de variations de f sur [0;]
3) Tracer la courbe sur l'intervalle [-2;2] en utilisant le 1).
Merci beaucoup !
Bonjour
1)La période de x -> cos(x) est 2pi celle de x -> cos(2x) est pi ; on pourrait donc l'étudier dans [0,2pi] ou [-pi,pi] mais comme c'est une fonction paire f(-x) = f(x) on peut l'étudier dans[0,pi]
2)f '(x) = 8.sin(x)+8.sin(2x) = 8.sin(x).(1 + 2cos(x)) et comme sin(x) est positif dans [0,pi] f '(x) est bien du signe de 1 + 2.cos(x)
f '(x) = 0 pour x = 2.pi/3 et f a 1 Max =~~7
.......> 0 .... x < ...... et f croît
.......< 0 .... x > ...... et f décroît
en 0 on a un minimum =~~-11 et en pi aussi =~~5
à +
Merci,je vois beaucoup mieux comment entamer le second exercice maintenant mais il y a un truc que je ne pige pas,c'est de construire la courbe sur l'intervalle donnée.
Bonsoir
Tu cherches qqes points f(0)=-11 ; f(pi/4)=1-4rac(2)=-4,65 ; f(pi/2)=5 ect
En bonus l'image
à+
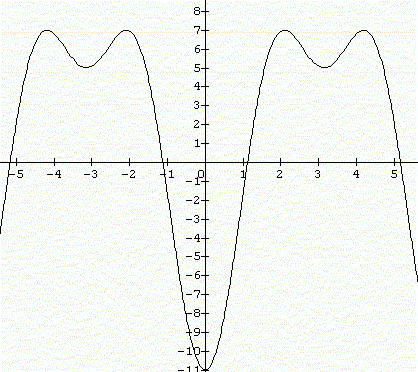
Merci mais enfait,ce que je n'ai pas compris,c'est l'intervalle utilisé.
Bonjour,
Pour ce qui concerne l'intervalle utilisé, je vais essayer de détailler l'explication déja donnée par geo3 :
La fonction x --> cos(x) a pour période 2.
La fonction x --> cos(2x) a pour période , car, d'une manière générale, si a>0, la fonction x-->cos(ax+b) a pour période 2/a.
La période est le plus petit multiple commun aux nombres et 2. La période est donc 2.
On peut donc, dans un premier temps, limiter l'étude de la fonction à un intervalle de largeur 2, par exemple l'intervalle [-;].
Il suffira ensuite, pour les autres périodes, de reproduire, par translation, le graphique dessiné sur cette période.
Par ailleurs, la fonction x-->cos(x) est paire. Cela signifie que cos(-x)=cos(x) et que, par conséquent, la courbe sera symétrique par rapport à l'axe des ordonnées.
On peut donc limiter l'intervalle d'étude à [0;] : l'autre moitié de la période sera obtenue par symétrie.
Annuler
connectez vous