Bonjour,

1. D'après le cours, à quelle condition un barycentre est-il défini ?

Bonsoir, si alfa + Beta + Gama # 0
C'est le cas c'est à partir de la deuxième question que je bloques.

2. Utilise le cours, et exprime le vecteur AK en fonction des vecteurs AB et AC. Conclus.

D'après le cours :

(k+1)KA + k²KB - k²KC = vecteur nul ( sachant que ici tout est vectoriel)
Si je développe :
(1+k)KA + k²(KA+AB) - k²(KA+AC) = vecteur nul
Et donc :
(1+k)KA + k²AB -k² AC = vecteur nul
Donc :
k²AB-k²AC = (1+k)AK

C'est ca ?

OK
Utilise la relation de Chasles dans le membre de gauche pour faire apparaître le vecteur CB

Je suis pas sure que ca marche...
Est ce que (1=k) milieu de CB ?

Je ne comprends pas ton message.
Utilise la relation de Chasles dans le membre de gauche pour faire apparaître le vecteur CB.

k²AB-k²AC = (1+k)AK
Donc :
k²AB - k²AC =(1+k)AK
k²AC + k² CB - k²AC = (1+k)AK
k² CB = (1+k) AK

Exprime le vecteur AK en fonction du vecteur CB. Conclus.

AK  = [k²/(1+k)] CB ?

OK. Donc... ?

Je n'arrive pas a conclure pour la simplification ..

Quelle simplification ?
AK = [k²/(1+k)] CB ?
donc K appartient à quelle demi-droite ?

Elle appartient a la demi droite CB ?

Je suis surpris que tu aies dit cela.
As-tu au moins fait une figure ?
Place les points A, B et C.
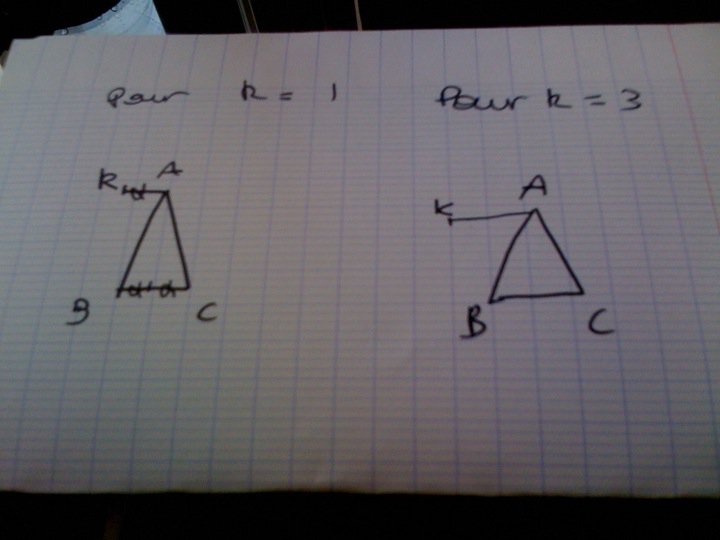
Place le point K en utilisant AK = [k²/(1+k)] CB avec différentes valeurs de k
Cela te donnera des idées si tu ne vois pas la conclusion tout de suite.

Donc k appartient a la demi droite AK ?

Evidemment que K appartient à la demi-droite [AK)
Tu es en train de dire que X et Y appartiennent à la droite (XY)...

As-tu au moins fait une figure ?
Place les points A, B et C.
Place le point K en utilisant AK = [k²/(1+k)] CB avec différentes valeurs de k
Cela te donnera des idées si tu ne vois pas la conclusion tout de suite.

Je suis désolée ...

J'ai essayé avec différentes valeurs
Mais pour moi k est appartient toujours a CB sur mon dessin

Peux-tu poster ton dessin, stp ?

Voila j'ai essayer avec k = 1 et k = 3

Ton positionnement de K sur la figure est faux. Regarde à nouveau

Ah, et la ?
Mais je ne vois toujours pas sur quelle droite se trouve le point K ..

C'est mieux.
Mais n'oublie pas que k est inférieur à -1.
Tu trouveras que K appartient à la demi-droite issue de A, parallèle à (BC) et allant dans la direction du vecteur BC ou CB (à toi de choisir).

Merci, je trouve ce sujet pas facile !

3. pour que AKCB existe il faut que vecteur
AK = BC

Certes.

C'est de cette maniere qu'il faut résonner pour repondre a la question ou non ?

C'est le tout début, oui.

3.
AKCB parallélogramme
<=> AK = BC (en vecteurs)
<=> AK = AC - AB
<=> K = Barycentre A,1 B,-1 C,1
<=> K = Barycentre A,-1 B,1 C,-1

Or K = Barycentre A;k+1 B;k² C;-k²

Il reste donc à voir s'il existe un k tel que k+1 = -k²

De quelle façon peut on vérifier cette égalité ?

C'est justement la question que je te pose.

Pour que k+1 = -k²
      <=> k = -k²-1 ?

C'est une équation du second degré. Tu dois savoir comment résoudre.

(k+1)+k² = 0
   Cette équation ne peut pas être égale a 0 car pour k = 0 Il restera toujours 1

Ou sinon  :
-k²-k=1
soit  -k(k+1)=1
soit  k(k+1)=-1 ?

Mais comme l'ensemble est ouvert en -1 il n'existe pas de solution a cette inéquation ?

Tu n'as pour l'instant rien démontré.
Vous avez vu en cours comment résoudre une équation du second degré ?
Résous cette équation.

3.
En fait, il serait un chouia plus naturel de démarrer ainsi :
K = Barycentre (A;k+1); (B;k²); (C;-k²)
Donc
AK = (k²/(k+1))AB - (k²/(k+1))AC (en vecteurs)
AK = (k²/(k+1))CB (en vecteurs)

AKCB parallélogramme
<=> AK = BC (en vecteurs)
<=> k²/(k+1) = -1
<=> k² = -k-1
<=> ...
(à continuer)

AKCB parallélogramme
<=> AK = BC (en vecteurs)
<=> k²/(k+1) = -1
<=> k² = -k-1
<=> k x k = -k - 1
<=> k = (-k-1)/ k
<=> k = -1 ?

Je ne comprends pas tes calculs.
C'est une bête équation du second degré. Résous-la.

Cette année je n'ai pas revu ca ..
Je ne connais plus vraiment la méthode..

Dans ce cas, révise ton cours de Seconde et reviens...

k² = -k-1
donc k² + k + 1 = 0
ET donc , l'équation n'a pas de solutions

Pourquoi n'a-t-elle pas de solution ?

Parceque k est défini sur l'ensemble] - l'infini ; -1 [

Et alors ? Je ne vois pas le rapport.
Je répète : résous cette équation du second degré.

k²/(k + 1) = -1
alors que I = ]moins l'infini; -1[
donc l'équation ne sera jamais égale à -1
car -1[
c'est exclu

En quoi le fait que k < -1 prouve-t-il que k²/(k + 1) < -1 ?
Montre ton calcul ou ton raisonnement.

f(-2), ca fait 4/-1 = -4
ensuite faut prouver que ca sera toujours moins
c'est simple, car K est toujours négatif
K² sera toujours positif
K + 1 sera toujours négatif
un positif divisé par un négatif = un négatif
donc ton equation aura toujours un resultat negatif

Oui, c'est toujours négatif.
Mais comment as-tu montré que c'est toujours < -1 ?