Bonjour à toutes et à tous.

Je bloque sur la question d'un exercice qui est le suivant :

Pour tout entier naturel n non nul, on considère la fonction fn définie sur ]0;+infini[ par fn(x) = ((ln x)^n)/x² et l'intégrale In = 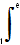fn(x) dx

1) On pose F(x) = (1+ln x)/x.  Calculer F'(x) et en déduire I1.

J'ai fais : F'(x) = [(1/x *x) - (1 + ln x)]/x² = (1 - 1 - ln x)/x² = -ln x/x²

I1 = 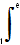f1(x) dx = 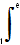(ln x)/x² dx = - [(1 +ln e)/e] - (ln 1 + 1)] = 1 - 2/e


2) Pour tout entier naturel n non nul, on définit sur [1; e] la fonction hn(x) = ((ln x)^n)/x. Calculer la fonction dérivée h'n+1 et en déduire que, pour tout entier naturel n non nul, In+1 = -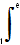h'n+1(x)dx + (n+1)*In puis que In+1 = -1/e + (n+1)In.

J'ai trouvé : h'n+1 = [(n+1)(ln x)^n -(ln x)^n+1]/x²

In+1 = -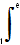 - (lnx)^(n+1)/x² dx = - 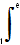h'n+1(x) dx + (n+1)*(ln x)^n/x²

In+1 = - [((ln e)^n+1 / e) - (ln 1)^n+1] + (n+1)In = -((ln e)^n+1)/e + (n+1)*In


3) Par définition, pour tout entier naturel n supérieur ou égal à 1, on a n! = 1*2*3*...*n

Montrer par récurrence que, pour tout entier naturel n non nul, (1/n!)*In = 1 - 1/e *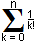

Initialisation : Pour n=1  •(1/n!)*In = In = 1-2/e  •1-1/e*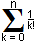= 1-1/e*(1+1) = 1-2/e

La propriété est vraie à son premier terme.

Hérédité : On suppose que (1/n!)*In = 1-1/e*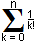
On souhaite démontrer que 1/(n+1) *In+1 = 1- 1/e *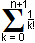

Là ça ne sert à rien de démontrer le calcul, à la fin je trouve exactement ce que je dois trouver ^^

4) Montrer que, pour tout n non nul, 0<(ou =) In <(ou =) 1

C'est là où je bloque, j'ai essayé la récurrence...je n'y suis pas parvenue...quelqu'un pourrait m'aider s'il vous plait ?

Merci beaucoup !
Bonne soirée.