Annuler
connectez vous
- Un petit Cours sur le cosinus - quatrième
- Trois Exercices sur le cosinus (différence entre un angle et son cosinus) - quatrième
- 10 Exercices sur les équations et les mises en équations - quatrième
- Six Exercices sur les pourcentages - quatrième
- Cours sur les fractions suivis de six Exercices - quatrième
- Exercice de Calcul avec des fractions - 4ème
- Sept Exercices sur les fractions - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième CosinusTopics traitant de cosinus [tout]Lister tous les topics de mathématiques
Niveau quatrième
Exercise DM cosinus d'un triangle.
Posté par jeremy54
Bonjour,j'ai eu un DM d'ont quelque exo que je n'arive pas :
1) a. construire un triangle MAI tel que AM= 6cm, AI= 9.1 cm, et IM= 10.9 cm.
b. quelle est la nature du triangle MAI ? justifier.
2) a. placer le point R appartenant au cote [MI] tel que MR= 8 cm.puis tracer la droite parralele a (AI) passant par R; elle coupe le cote [AM] en E.
b. quelle est la nature du triangle MER ? justifier.
3) a. exprimer cos AMI de deux manieres differentes .
b. en deduire ME. on donnera l'arrondi au millimetre.
Bonjour
Q1 / Ds ce type de question, 3 réflexes à avoir
- les 3 côtés du trg ne sont pas égaux, dc le trg n'est pas équilatéral
- il n'y a pas 2 côtés de même longueur, dc le trg n'est pas isocèle
- on vérifie alors si la somme des carrés des deux plus petites mesures des côtés ne serait pas égale au carré de la mesure du + grand côté, pr vérifier si ce trg ne serait pas un trg rectangle.
On a bien 6² + 9.1² = 10.9² (vérifie à la calculatrice), et dc la réciproque du tm de Pythagore permet d'affirmer que le trg MAI est un trg rectangle en A.
D'accord ?
Bonjour,
As-tu essayé de le faire ?
telle que la 1ère question est posée, à priori, cela ne peut qu'être un triangle rectangle.
Il te faut donc vérifier la réciproque du théorême de Pythagore càd
est-ce que 10,9²=6²+9,1²
je te laisse faire cette vérification
pour la seconde question tu te sers de la propriété suivante
si une droite d est perpendiculaire à une droite d', alors toute paralléle à d sera également perpendiculaire à d'
et pour la dernière question, tu as appris que le cosinus d'un angle dans un triangle rectangle est égal au rapport
(côté adjacent)/hypoténuse
donc ici au rapport AM/MI
et puisque les droites (AM) et (RE) sont parallèles l'angle EMI est égal à l'angle AMI (correspondants)
et dans le triangle ERI
cosERI=cosAMI=EI/RI=AM/MI
tu peux calculer RI= (MI-MR); tu connais donc tout à l'exception de ME dans l'égalité des rapports de la ligne précédente
et tu peux donc calculer ME
Q2a
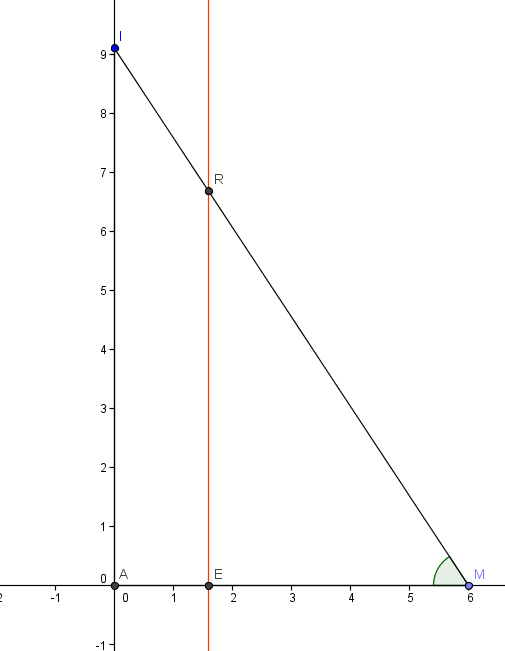
Q2b
On sait que MAI est un trg rectangle en A (CfQ1), dc (AI)
(AM)
D'après l'énoncé, (ER)//(AI), dc (ER)(AM) (Tm: Ds le plan, lorsqu'une droite (A) est perpendiculaire à une autre droite (B), toute droite // à (A) est perpendiculaire à (B).
Le point E 
(AM), dc (ER)(EM).
On en conclut que le trg MER est un trg rectangle en E.
Q3a
Ds un trg rectangle, le cosinus d'un angle est égal au rapport de la mesure du côté adjacent à cet angle sur la mesure de l'hypoténuse du trg rectangle.
Ici, le côté adjacent à est [AM] et l'hypoténuse [MI]
On a dc
OR, (Cf schéma), .
Q3b
et sachant que , on en déduit :
On en déduit :
D'accord ?
A ta disposition si tu as des questions